
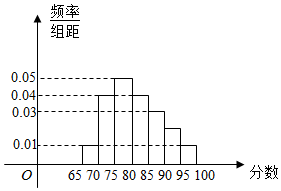
 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的人数为19.
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的人数为19.分析 (1)先求出80~90分数段频率和此分数段的学员总数,由此能求出毕业生的总人数;求出90~95分数段内的人数频率,由此能求出90~95分数段内的人数.
(2)90~95分数段内的4 人中有2名男生,2名女生,设男生 为A1,A2;女生 为B1,B2,设安排结果中至少有一名男生为事件A,由此利用列举法能求出安排结果至少有一名男生的概率.
解答 解:(1)80~90分数段频率为p1=(0.04+0.03)×5=0.35,
此分数段的学员总数为14,
∴毕业生的总人数N为40…(3分)
90~95分数段内的人数频率为p2=1-(0.01+0.04+0.05+0.04+0.03+0.01)×5=0.1,
∴90~95分数段内的人数n=40×0.1=4.…(6分)
(2)90~95分数段内的4 人中有2名男生,2名女生,
设男生 为A1,A2;女生 为B1,B2,设安排结果中至少有一名男生为事件A,
从中取两名毕业生的所有情况(基本事件空间)为A1A2,A1B1,A1B2,A2B1,A2B2,B1B2共6种组合方式,…(9分)
其中,至少有一名男生的种数为A1A2,A1B1,A1B2,A2B1,A2B2共5种,
∴安排结果至少有一名男生的概率$P(A)=\frac{5}{6}$…..(12分)
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:解答题
 如图,等腰梯形ABCD中,AB∥CD,DE⊥AB于E,CF⊥AB于F,且AE=BF=EF=2,DE=CF=2.将△AED和△BFC分别沿DE,CF折起,使A,B两点重合,记为点M,得到一个四棱锥M-CDEF,点G,N,H分别是MC,MD,EF的中点.
如图,等腰梯形ABCD中,AB∥CD,DE⊥AB于E,CF⊥AB于F,且AE=BF=EF=2,DE=CF=2.将△AED和△BFC分别沿DE,CF折起,使A,B两点重合,记为点M,得到一个四棱锥M-CDEF,点G,N,H分别是MC,MD,EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 锐角或钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞成禁放 | 不赞成禁放 | 合计 | |
| 老年人 | 60 | 140 | 200 |
| 中青年人 | 80 | 120 | 200 |
| 合计 | 140 | 260 | 400 |
| P(k2>k0) | 0.050 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 内部 | B. | 圆上 | C. | 外部 | D. | 与θ相关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com