
| A. | $\frac{8}{5}$ | B. | $\frac{5}{8}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
分析 利用向量共线求出正切函数值,化简所求表达式为正切函数的形式,代入求解即可.
解答 解:向量$\overrightarrow m$=($\sqrt{3}$sinx,cosx),$\overrightarrow n$=(2$\sqrt{3}$,1),且$\overrightarrow m$∥$\overrightarrow n$,
可得$\sqrt{3}$sinx=2$\sqrt{3}$cosx,即tanx=2.
$\frac{{2{{cos}^2}x+sin2x}}{1+tanx}$=$\frac{2co{s}^{2}x+2sinxcosx}{(si{n}^{2}x+co{s}^{2}x)(1+tanx)}$=$\frac{2+2tanx}{(ta{n}^{2}x+1)(1+tanx)}$=$\frac{2}{4+1}$=$\frac{2}{5}$.
故选:C.
点评 本题考查向量的共线以及三角函数的化简求值,考查计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≥0} | B. | {x|x≥1} | C. | {x|x>0}∪{0} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程x3+ax-b=0没有实根 | B. | 方程x3+ax-b=0至多有一个实根 | ||
| C. | 方程x3+ax-b=0至多有两个实根 | D. | 方程x3+ax-b=0恰好有两个实根 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
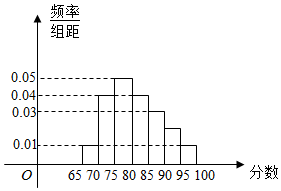 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的人数为19.
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的人数为19.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{asinαsinβ}{sin(α-β)}$ | B. | $\frac{asinαsinβ}{cos(α-β)}$ | C. | $\frac{acosαcosβ}{sin(α-β)}$ | D. | $\frac{acosαcosβ}{cos(α-β)}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com