
已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.
(1)求C的方程;
(2)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
解 (1)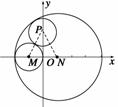 设圆P的半径为r,则|PM|=1+r,|PN|=3-r,∴|PM|+|PN|=4>|MN|,∴P的轨迹是以M,N为焦点的椭圆(左顶点除外),且2a=4,2c=2,∴a=2,c=1,∴b2=a2-c2=3.
设圆P的半径为r,则|PM|=1+r,|PN|=3-r,∴|PM|+|PN|=4>|MN|,∴P的轨迹是以M,N为焦点的椭圆(左顶点除外),且2a=4,2c=2,∴a=2,c=1,∴b2=a2-c2=3.
∴P的轨迹曲线C的方程为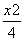 +
+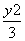 =1(x≠-2).
=1(x≠-2).
(2)由(1)知2r=(|PM|-|PN|)+2≤|MN|+2=4,
∴圆P的最大半径为r=2.此时P的坐标为(2,0).
圆P的方程为(x-2)2+y2=4.
①当l的倾斜角为90°,方程为x=0时,|AB|=2 ,
,
②当l的倾斜角不为90°,
设l的方程为y=kx+b(k∈R),
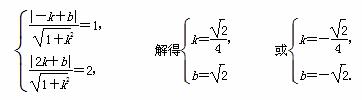 ∴l的方程为y=
∴l的方程为y=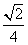 x+
x+ ,y=-
,y=-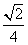 x-
x- .
.
联立方程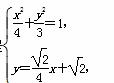 化简得7x2+8x-8=0,
化简得7x2+8x-8=0,
∴x1+x2=-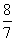 ,x1x2=-
,x1x2=-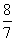 ,
,
∴|AB|=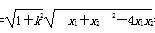 =
= .
.
当k=-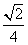 时,由图形的对称性可知|AB|=
时,由图形的对称性可知|AB|= .
.
综上,|AB|=2 或
或 .
.


科目:高中数学 来源: 题型:
已知双曲线的方程为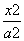 -
-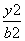 =1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为
=1(a>0,b>0),双曲线的一个焦点到一条渐近线的距离为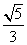 c(其中c为双曲线的半焦距长),则该双曲线的离心率为( ).
c(其中c为双曲线的半焦距长),则该双曲线的离心率为( ).
A.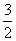 B.
B.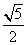 C.
C.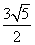 D.
D.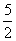
查看答案和解析>>
科目:高中数学 来源: 题型:
已知圆C经过A(5,2),B(-1,4)两点,圆心在x轴上,则圆C的方程是( ).
A.(x-2)2+y2=13 B.(x+2)2+y2=17
C.(x+1)2+y2=40 D.(x-1)2+y2=20
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C: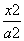 +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为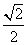 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为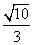 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,椭圆C: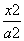 +
+ =1(a>b>0)经过点P
=1(a>b>0)经过点P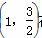 ,离心率e=
,离心率e=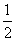 ,直线l的方程为x=4.
,直线l的方程为x=4.

(1)求椭圆C的方程;
(2)AB是经过右焦点F的任一弦(不经过点P),设直线AB与直线l相交于点M,记PA,PB,PM的斜率分别为k1,k2,k3.问:是否存在常数λ,使得k1+k2=λk3?若存在,求λ的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
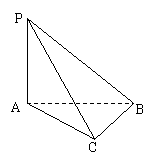
三棱锥P−ABC中,PA⊥平面ABC,AB⊥BC。
(1)证明:平面PAB⊥平面PBC;
(2)若PA=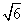 ,PC与侧面APB所成角的余弦值为
,PC与侧面APB所成角的余弦值为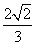 ,
,
PB与底面ABC成60°角,
求二面角B―PC―A的大小。
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com