
【题目】已知数列{an},{bn}满足2Sn=(an+2)bn,其中Sn是数列{an}的前n项和.
(1)若数列{an}是首项为![]() ,公比为-
,公比为-![]() 的等比数列,求数列{bn}的通项公式;
的等比数列,求数列{bn}的通项公式;
(2)若bn=n,a2=3,求证:数列{an}满足an+an+2=2an+1,并写出数列{an}的通项公式.
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD= ![]() AD.E为棱AD的中点,异面直线PA与CD所成的角为90°.
AD.E为棱AD的中点,异面直线PA与CD所成的角为90°. 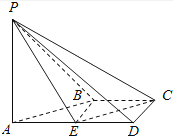
(1)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(2)若二面角P﹣CD﹣A的大小为45°,求直线PA与平面PCE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题中:
①命题: ![]() ;
;
②函数f(x)=2x﹣x2有三个零点;
③对(x,y)∈{(x,y)|4x+3y﹣10=0},则x2+y2≥4.
④已知函数 ![]() ,若△ABC中,角C是钝角,那么f(sinA)>f(cosB)
,若△ABC中,角C是钝角,那么f(sinA)>f(cosB)
其中所有真命题的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 C:![]() 离心率
离心率![]() ,短轴长为
,短轴长为![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)如图,椭圆左顶点为A,过原点O的直线![]() (与坐标轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点.试问以MN为直径的圆是否经过定点?请证明你的结论.
(与坐标轴不重合)与椭圆C交于P,Q两点,直线PA,QA分别与y轴交于M,N两点.试问以MN为直径的圆是否经过定点?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() 过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.
过点M(2,0),且右焦点为F(1,0),过F的直线l与椭圆C相交于A、B两点.设点P(4,3),记PA、PB的斜率分别为k1和k2.

(1)求椭圆C的方程;
(2)如果直线l的斜率等于-1,求出k1k2的值;
(3)探讨k1+k2是否为定值?如果是,求出该定值;如果不是,求出k1+k2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga![]() (a>0且a≠1)是奇函数,
(a>0且a≠1)是奇函数,
(1)求实数m的值;
(2)若a=![]() ,并且对区间[3,4]上的每一个x的值,不等式f(x)>(
,并且对区间[3,4]上的每一个x的值,不等式f(x)>(![]() )x+t恒成立,求实数t的取值范围.
)x+t恒成立,求实数t的取值范围.
(3)当x∈(r,a-2)时,函数f(x)的值域是(1,+∞),求实数a与r的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1) 把![]() 的图象上每一点的纵坐标变为原来的
的图象上每一点的纵坐标变为原来的![]() 倍,再将横坐标向右平移
倍,再将横坐标向右平移![]() 个单位,可得
个单位,可得![]() 图象,求
图象,求![]() ,
,![]() 的值;
的值;
(2) 若对任意实数![]() 和任意
和任意![]() ,恒有
,恒有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的奇函数f(x)的周期为4,且x∈(0,2)时f(x)=ln(x2﹣x+b),若函数f(x)在区间[﹣2,2]上恰有5个零点,则实数b应满足的条件是( )
A.﹣1<b≤1
B.﹣1<b<1或b= ![]()
C.![]() <b
<b ![]()
D.![]() <b≤1或b=
<b≤1或b= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com