
分析 (Ⅰ)根据f(x)为奇函数,便有f(0)=0,这便得到b=0,再根据f$(\frac{1}{2})$=$\frac{2}{5}$即可求出a=1,从而得出f(x)的解析式;
(Ⅱ)求f′(x)=$\frac{1-{x}^{2}}{({x}^{2}+1)}$,容易判断f′(x)>0,从而知道f(x)在(-1,1)上单调递增,而将原不等式变成f(t-1)<f(-t),这便得到$\left\{\begin{array}{l}{-1<t-1<1}\\{-1<-t<1}\\{t-1<-t}\end{array}\right.$,解该不等式组即得原不等式的解.
解答 解:(Ⅰ)因为f(x)为奇函数,且在x=0有定义;
∴f(0)=b=0;
又$f(\frac{1}{2})=\frac{2}{5}$,即$\frac{{\frac{1}{2}a}}{{{{({\frac{1}{2}})}^2}+1}}=\frac{2}{5}$;
解得a=1;
∴$f(x)=\frac{x}{{{x^2}+1}}$;
(Ⅱ)由(Ⅰ)得,$f'(x)=\frac{{1-{x^2}}}{{{{({{x^2}+1})}^2}}}$;
∵x∈(-1,1),0≤x2<1,1-x2>0;
∴f'(x)>0,即f(x)在(-1,1)上单调递增;
由f(t-1)+f(t)<0,得f(t-1)<-f(t)=f(-t);
∴$\left\{{\begin{array}{l}{-1<t-1<1}\\{-1<-t<1}\\{t-1<-t}\end{array}}\right.$;
解得$0<t<\frac{1}{2}$;
∴原不等式解集为(0,$\frac{1}{2}$).
点评 考查奇函数在原点有定义时,f(0)=0,根据导数符号判断函数单调性的方法,商的求导公式,以及奇函数的定义的运用.


科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (1,5) | C. | (2,3) | D. | (2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 垂心 | B. | 外心 | C. | 内心 | D. | 重心 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
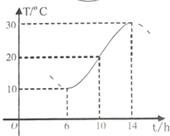 如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].
如图,某地一天从6-14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π),则该函数的表达式为y=10sin($\frac{π}{8}$x+$\frac{3π}{4}$)+20,x∈[6,14].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com