
分析 先求出p,q为真时的a的范围,如果“p且q”为真命题,“p,q”也为真命题,则“p或q”为假命题.,“p,q”都假,即可求解.
解答 解:对于命题p:由a2x2-ax-2=0在[-1,1]上有解,
当a=0时,不符合题意;
当a≠0时,方程可化为:(ax-2)(ax+1)=0,
解得:x=$\frac{2}{a}$,或x=-$\frac{1}{a}$,
∵x∈[-1,1],
∴-1≤$\frac{2}{a}$≤1或-1≤-$\frac{1}{a}$≤1,
解得:a≥2或a≤-2
对于命题q:由只有一个实数x满足不等式x2+2ax+2a≤0
得抛物线y=x2+2ax+2a与x轴只有一个交点,
∴△=4a2-8a=0
∴a=0或a=2
(1)若“p且q”是真命题,则a=2,
(2)若“p或q”是假命题,则-2<a<2且a≠0.
点评 由简单命题和逻辑连接词构成的复合命题的真假可以用真值表来判断,反之根据复合命题的真假也可以判断简单命题的真假.假若p且q真,则p 真,q也真;若p或q真,则p,q至少有一个真;若p且q假,则p,q都假,本题属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 所有的实数x都能使x+$\frac{1}{x}$≥2成立 | |
| B. | 存在一个实数x使不等式x2-2x+3<0成立 | |
| C. | 如果x、y 是实数,那么“xy>0”是“|x+y|=|x|+|y|”的充分但不必要条件 | |
| D. | 命题甲:“a、b、c”成等差数列”是命题乙:“$\frac{a}{b}+\frac{c}{b}$=2”的充要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
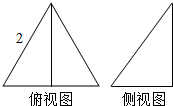 已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.
已知一个三棱锥的俯视图与侧(左)视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的表面积为$\sqrt{19}+\sqrt{3}+2$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com