
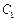 和抛物线
和抛物线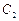 有公共焦点F(1,0),
有公共焦点F(1,0), 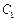 的中心和
的中心和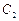 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线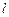 与抛物线
与抛物线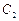 分别相交于A,B两点.
分别相交于A,B两点.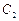 的标准方程;
的标准方程;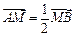 ,求直线
,求直线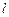 的方程;
的方程;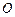 关于直线
关于直线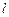 的对称点
的对称点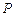 在抛物线
在抛物线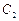 上,直线
上,直线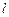 与椭圆
与椭圆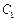 有公共点,求椭圆
有公共点,求椭圆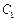 的长轴长的最小值.
的长轴长的最小值. 名校通行证有效作业系列答案
名校通行证有效作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com