练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知椭圆的中心在原点，焦点在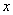轴上，长轴长是短轴长的2倍且经过点M(2,1)，平行于OM的直线l在轴上的截距为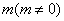，l交椭圆于A、B两个不同点.

    （1）求椭圆的方程；

    （2）求m的取值范围；

    （3）求证直线MA、MB与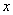轴始终围成一个等腰三角形.

     


    解：（1）设椭圆方程为

        则

        ∴椭圆方程

       （2）∵直线l平行于OM，且在轴上的截距为m

    又

    ∴l的方程为：

    由

    ∵直线l与椭圆交于A、B两个不同点，

        ∴m的取值范围是

       （3）设直线MA、MB的斜率分别为k1，k2，只需证明k1＋k2=0即可

        设

        可得

       

        而

       

       

        ∴k1＋k2=0

        故直线MA、MB与x轴始终围成一个等腰三角形.  


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    某地区高中分三类，A类学校共有学生2 000人，B类学校共有学生3 000人，C类学校共有学生4 000人，若采取分层抽样的方法抽取900人，则A类学校中应抽学生人数是(　　)

    A．300      B．200      C．150      D．100

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    阅读如图所示的程序框图，若输入的k＝10，则该算法的功能是(　　)

    A．计算数列{2n－1}的前10项和

    B．计算数列{2n－1}的前9项和

    C．计算数列{2n－1}的前10项和

    D．计算数列{2n－1}的前9项和

    解析：第一次循环：S＝1，i＝2，i<10；

    第二次循环：S＝3，i＝3，i<10；

    第三次循环：S＝7，i＝4，i<10

    ……

    第九次循环：S＝29－1，i＝10，i＝10.

    第十次循环：S＝210－1，i＝11，i>10，输出S.

    根据选项，S＝，故为数列{2n－1}的前10项和．故选A.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过点(2,-1)引直线与抛物线只有一个公共点,这样的直线共有(   )条

    A.  1            B.2              C. 3           D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    双曲线与椭圆有相同焦点，且经过点，求其方程。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    以正方形的顶点为顶点的三棱锥的个数   (    ）

    A．   B． C．      D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    二项式的展开式中常数项为           ；

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从甲，乙，丙，丁4个人中随机选取两人，则甲乙两人中有且只有一个被选取的概率为  

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知复数满足（i为虚数单位），则z的值为

    A．i            B．－i              C．1            D．－1

    查看答案和解析>>

    同步练习册答案