练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    .如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC,如图2所示.

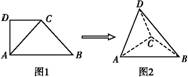
    (1)求证:BC⊥平面ACD;

    (2)求几何体DABC的体积.


     (1)证明:在题图1中,

    可得AC=BC=2,

    从而AC2+BC2=AB2,

    故AC⊥BC,

    取AC的中点O,连接DO,

    则DO⊥AC,

    又平面ADC⊥平面ABC,平面ADC∩平面ABC=AC,

    DO⊂平面ADC,

    从而DO⊥平面ABC,

    ∴DO⊥BC,

    又AC⊥BC,AC∩DO=O,

    ∴BC⊥平面ACD.

    (2)解:由(1)可知,BC为三棱锥BACD的高,BC=2,S△ACD=2,

    ∴=

    =S△ACD·BC

    =×2×2

    =.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知点是如图所示平面区域内的任意一点，则的取值范围为          .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一几何体的三视图如图所示,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何体(图形)可能是( )

    ①矩形;②有三个面为直角三角形,有一个面为等腰三角形的四面体;③每个面都是直角三角形的四面体.

    (A)①②③   (B)②③ (C)①③ (D)①②

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图是一个几何体的三视图,正视图和侧视图均为矩形,俯视图中曲线部分为半圆,尺寸如图,则该几何体的表面积为(　　)

    (A)2+3π+4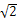    (B)2+2π+4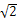

    (C)8+5π+2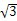    (D)6+3π+2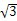

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某几何体的三视图如图所示,则该几何体的体积是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正方体ABCDA1B1C1D1中,O是BD1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是( 　)

    (A)A1、M、O三点共线

    (B)M、O、A1、A四点共面

    (C)A、O、C、M四点共面

    (D)B、B1、O、M四点共面

    查看答案和解析>>

    科目：高中数学 来源： 题型：


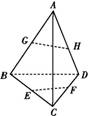
    如图所示 ,在四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=DH∶HA=2∶3.求证:EF、GH、BD交于一点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,几何体EABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.

    (1)求证:BE=DE;

    (2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在四棱锥PABCD中,底面ABCD是正方形,侧棱PD⊥平面ABCD,AB=PD=a.点E为侧棱PC的中点,又作DF⊥PB交PB于点F.则PB与平面EFD所成角为(　)

    (A)30° (B)45° (C)60° (D)90°

    查看答案和解析>>

    同步练习册答案