
����Ŀ�����й����ʽ��ڲ�������2018��11��5�ա�10�����Ϻ����һ�չ���ľٰ졣�����ڼ�,ij��˾���ɹ�������ijˮ����ֲ���ص�ˮ������˾���ܾ��������ֲ���صĸ����˳��ϰ��̶�һ���Բɹ�һ��ˮ���IJɹ���![]() ��Ԫ/�֣���ɹ���
��Ԫ/�֣���ɹ���![]() ���֣�֮��ĺ�����ϵ��ͼ����ͼ�е�����
���֣�֮��ĺ�����ϵ��ͼ����ͼ�е�����![]() ��ʾ���������˵�
��ʾ���������˵�![]() ���������˵�
���������˵�![]() ��.
��.
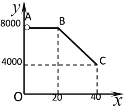
������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
������֪��ˮ����ֲ������ֲ��ˮ���ijɱ���2800Ԫ/�֣���ô���ܾ����IJɹ���Ϊ����ʱ����ˮ��������������������������![]() �����������Ƕ��٣�
�����������Ƕ��٣�
���𰸡�(��)![]() ��
��![]() �������������Ϊ105800Ԫ
�������������Ϊ105800Ԫ
��������
���ֶκ��������ʽ��
�������ö��κ�������ֵ, ��òɹ���Ϊ����ʱ�������������.
(��)��![]() ʱ��
ʱ�� ![]()
��![]() ʱ����
ʱ����![]() ����ĺ�����ϵʽΪ
����ĺ�����ϵʽΪ![]() ��
��
��![]() �����
�����![]() ������
������![]()
���ϣ�![]()
![]()
����![]() ʱ����ˮ����ֲ���ػ�õ�����
ʱ����ˮ����ֲ���ػ�õ�����![]() ��
��
��ʱ��ˮ����ֲ���ػ�õ��������Ϊ104000Ԫ ����![]() ʱ����ˮ����ֲ���ػ�õ�����Ϊ
ʱ����ˮ����ֲ���ػ�õ�����Ϊ![]()
���Ե�![]() ʱ������
ʱ������![]() ȡ�����ֵ�����ֵΪ105800Ԫ����Ϊ
ȡ�����ֵ�����ֵΪ105800Ԫ����Ϊ![]() ��
��
���Ե��������ɹ���Ϊ23��ʱ����ˮ����ֲ�������������������õ���������������Ϊ105800Ԫ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڣ����ޣ�0���ȣ�0��+�ޣ��ϵĺ���f��x�������������������ĵȱ�����{an}��{f��an��}���ǵȱ����У����f��x��Ϊ�����ȱ����к����������ж����ڣ����ޣ�0���ȣ�0��+�ޣ��ϵ����º�������f��x��=x2����f��x��=2x����f��x��= ![]() ����f��x��=ln|x|���������ǡ����ȱ����к�������f��x�������Ϊ�� ��
����f��x��=ln|x|���������ǡ����ȱ����к�������f��x�������Ϊ�� ��
A.�٢�
B.�ۢ�
C.�٢�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ�������![]() .��
.��![]()
(1)��![]() �Ľ���ʽ��
�Ľ���ʽ��
(2)��������[-1,1]�ϲ���ʽ![]() ���������ʵ��m��ȡֵ��Χ.
���������ʵ��m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������C��x2=2py��p��0���Ľ���ΪF����Ϊl��A��C����֪��FΪԲ�ģ�FAΪ�뾶��ԲF��l��B��D���㣻
��1������BFD=90�㣬��ABD�����Ϊ ![]() ����p��ֵ��ԲF�ķ��̣�
����p��ֵ��ԲF�ķ��̣�
��2����A��B��F������ͬһֱ��m�ϣ�ֱ��n��mƽ�У���n��Cֻ��һ�������㣬������ԭ�㵽m��n����ı�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
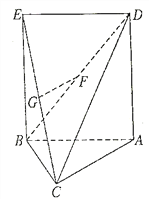
����Ŀ����ͼ����![]() �У�
�У� ![]() ���ı���
���ı���![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �������Σ�ƽ��
�������Σ�ƽ��![]() ƽ��
ƽ��![]() ����
����![]() ��
�� ![]() �ֱ���
�ֱ���![]() ���е�.
���е�.
��1����֤�� ![]() ƽ��
ƽ��![]() ;
;
��2����֤��ƽ��![]() ƽ��
ƽ��![]() ;
;
��3������![]() �����
�����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ����������,��![]() �DZ߳�Ϊ2��������,��
�DZ߳�Ϊ2��������,��![]() ��ֱ������,
��ֱ������,![]() ��
��![]() .
.
(1)��֤:![]() ƽ��
ƽ��![]() ��
��
(2)�������![]() Ϊ60��,��ֱ��
Ϊ60��,��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ��![]() ��
��![]() �յġ�ȫ�����ա���ij��ѧѧ�����ȫ�������������ȡ
�յġ�ȫ�����ա���ij��ѧѧ�����ȫ�������������ȡ![]() �������μ�
�������μ�![]() ���г��ܲ��ԣ������Եõ�ÿ���������ܲ�����ʱ��ľ�Ҷͼ��С����ǰһλ����Ϊ����С����ĺ�һλ����ΪҶ������ͼ�����ܲ�ʱ�䲻����
���г��ܲ��ԣ������Եõ�ÿ���������ܲ�����ʱ��ľ�Ҷͼ��С����ǰһλ����Ϊ����С����ĺ�һλ����ΪҶ������ͼ�����ܲ�ʱ�䲻����![]() �룬���Ϊ�������ܡ�.
�룬���Ϊ�������ܡ�.
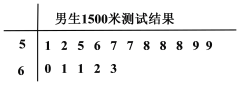
���� д���������ݵ���������λ����
����Ҫ���� ![]() �������ѡȡ
�������ѡȡ![]() �ˣ���������
�ˣ���������![]() ���ǡ������ܡ��ĸ��ʣ�
���ǡ������ܡ��ĸ��ʣ�
�������� ![]() �˵�������������������ѧУ�������������ݣ����Ӹ�У�����������ڶࣩ��ȡ
�˵�������������������ѧУ�������������ݣ����Ӹ�У�����������ڶࣩ��ȡ![]() �ˣ���
�ˣ���![]() ��ʾ�鵽�������ܡ�ѧ������������
��ʾ�鵽�������ܡ�ѧ������������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A-EFCB�У�![]() Ϊ�ȱ������Σ�ƽ��AEF
Ϊ�ȱ������Σ�ƽ��AEF![]() ƽ��EFCB��
ƽ��EFCB��![]() ��
��![]() ��
��![]() ��
��![]() ��OΪEF���е㣮
��OΪEF���е㣮
������֤��![]() ��
��
����������F-AE-B������ֵ��
������BE![]() ƽ��AOC����a��ֵ��
ƽ��AOC����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �Ƕ�����
�Ƕ�����![]() �ϵĺ���.��������
�ϵĺ���.��������![]() ��ʹ
��ʹ![]() ����������
����������![]() ��
��![]() �ϵ�����������������
�ϵ�����������������![]() ��ʹ
��ʹ![]() ����������
����������![]() ��
��![]() �ϲ����ܵ����ݼ�����������
�ϲ����ܵ����ݼ�����������![]() ��������
��������![]() ����
����![]() ����������
����������![]() ��
��![]() �ϵ�������.��������˵����ȷ����_________.����д��ţ�
�ϵ�������.��������˵����ȷ����_________.����д��ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com