
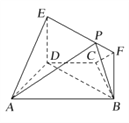
【题目】如图,在四棱锥A-EFCB中,![]() 为等边三角形,平面AEF
为等边三角形,平面AEF![]() 平面EFCB,
平面EFCB,![]() ,
,![]() ,
,![]() ,
,![]() ,O为EF的中点.
,O为EF的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角F-AE-B的余弦值;
(Ⅲ)若BE![]() 平面AOC,求a的值.
平面AOC,求a的值.
【答案】(I)证明见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】
(I)由于平面AEF![]() 平面EFCB,
平面EFCB,![]() 为等边三角形,O为EF的中点,则
为等边三角形,O为EF的中点,则![]() ,根据面面垂直性质定理,所以AO
,根据面面垂直性质定理,所以AO![]() 平面EFCB,又
平面EFCB,又![]() 平面EFCB,则
平面EFCB,则![]() .
.
(II) 取CB的中点D,链接OD,以O为原点,分别以OE,OD,OA为x,y,z轴建立空间直角坐标系,A![]() ,E
,E![]() ,B
,B![]() ,
,![]()
![]() ,
,![]() ,由于平面AEF与Y轴垂直,则设平面AEF的法向量为
,由于平面AEF与Y轴垂直,则设平面AEF的法向量为![]() ,设平面AEB的法向量
,设平面AEB的法向量![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,y=-1,则
,y=-1,则![]() ,二面角F-AE-B的余弦值cos(
,二面角F-AE-B的余弦值cos(![]() ,
,![]() )=
)=![]() =
=![]() ,由二面角F-AE-B为钝二面角,所以二面角F-AE-B的余弦值为
,由二面角F-AE-B为钝二面角,所以二面角F-AE-B的余弦值为![]() .
.
(Ⅲ)由(I)知![]() 平面EFCB,则
平面EFCB,则![]() ,若
,若![]() 平面
平面![]() ,只需
,只需![]() ,
,![]() ,又
,又![]() ,
,![]() ,解得
,解得![]() 或
或![]() ,由于
,由于![]() ,则
,则![]() .
.
【考点精析】利用向量语言表述线线的垂直、平行关系对题目进行判断即可得到答案,需要熟知设直线![]() 的方向向量分别是
的方向向量分别是![]() ,则要证明
,则要证明![]() ∥
∥![]() ,只需证明
,只需证明![]() ∥
∥![]() ,即
,即![]() ;则要证明
;则要证明![]() ,只需证明
,只需证明![]() ,即
,即![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个顶点为
的一个顶点为![]() ,且它的离心率与双曲线
,且它的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆的方程;
(2)过点A且斜率为k的直线l与椭圆相交于A,B两点,点M在椭圆上,且满![]() 求k的值.
求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】首届中国国际进口博览会在2018年11月5日—10日在上海国家会展中心举办。会议期间,某公司欲采购东南亚某水果种植基地的水果,公司刘总经理与该种植基地的负责人陈老板商定一次性采购一种水果的采购价![]() (元/吨)与采购量
(元/吨)与采购量![]() (吨)之间的函数关系的图象如图中的折线
(吨)之间的函数关系的图象如图中的折线![]() 所示(不包含端点
所示(不包含端点![]() ,但包含端点
,但包含端点![]() ).
).
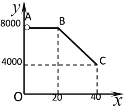
(Ⅰ)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(Ⅱ)已知该水果种植基地种植该水果的成本是2800元/吨,那么刘总经理的采购量为多少时,该水果基地在这次买卖中所获得利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() .
.
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形ABCD沿对角线BD折成直二面角A﹣BC﹣C,有如下四个结论:
①AC⊥BD;②△ABC是等边三角形;
③AB与CD所成的角90°;④二面角A﹣BC﹣D的平面角正切值是![]() ;
;
其中正确结论是 .(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数f(x)=2a2x-1-1的图象过定点(![]() ,-1);
,-1);
②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.
③若loga![]() >1,则a的取值范围是(
>1,则a的取值范围是(![]() ,1);
,1);
④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;
⑤对于函数f(x)=lnx,其定义域内任意x1≠x2都满足f(![]() )≥
)≥![]()
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京、张家口2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量![]() 至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com