练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若二次函数满足.且

    (1)求的解析式；

    (2)若在区间[-1,1]上不等式恒成立，求实数m的取值范围.

    【答案】（1）；（2）

    【解析】

    （1）利用待定系数法求解．由二次函数可设f（x）＝ax2+bx+c，由f（0）＝1得c值，由f（x+1）﹣f（x）＝2x可得a，b的值，从而问题解决；

    （2）欲使在区间[﹣1，1]上不等式f（x）＞2x+m恒成立，只须x2﹣3x+1﹣m＞0，也就是要x2﹣3x+1﹣m的最小值大于0即可，最后求出x2﹣3x+1﹣m的最小值后大于0解之即得．

    （1）设二次函数，

    则

    又

    即

    解得

    （2）不等式化为

    在区间[-1,1]上不等式恒成立

    在区间[-1,1]上不等式恒成立

    只需在区间[-1,1]上，函数是减函数

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，ξ=0；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，ξ=1．
    （1）求概率P（ξ=0）；
    （2）求ξ的分布列，并求其数学期望E（ξ）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面是梯形，，，，.

    （1）证明：平面平面；

    （2）若与平面所成的角为，，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个顶点为,且它的离心率与双曲线的离心率互为倒数.

    (1)求椭圆的方程;

    (2)过点A且斜率为k的直线l与椭圆相交于A,B两点,点M在椭圆上,且满求k的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是定义在上的奇函数，且，对任意的且 时，有成立．

    （1）判断在上的单调性，并用定义证明；

    （2）解不等式；

    （3）若对任意的恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2019年是中华人民共和国成立70周年，某校党支部举办了一场“我和我的祖国”知识竞赛，满分100分，回收40份答卷，成绩均落在区间内，将成绩绘制成如下的频率分布直方图.

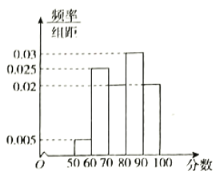
    （1）估计知识竞赛成绩的中位数和平均数；

    （2）从，分数段中，按分层抽样随机抽取5份答卷，再从对应的党员中选出3位党员参加县级交流会，求选出的3位党员中有2位成绩来自于分数段的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设F为抛物线C：y2=4x的焦点，过点P（﹣1，0）的直线l交抛物线C于两点A，B，点Q为线段AB的中点，若|FQ|=2，则直线l的斜率等于 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】首届中国国际进口博览会在2018年11月5日—10日在上海国家会展中心举办。会议期间,某公司欲采购东南亚某水果种植基地的水果，公司刘总经理与该种植基地的负责人陈老板商定一次性采购一种水果的采购价（元/吨）与采购量（吨）之间的函数关系的图象如图中的折线所示（不包含端点，但包含端点）.

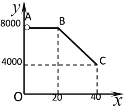
    （Ⅰ）求与之间的函数关系式；

    （Ⅱ）已知该水果种植基地种植该水果的成本是2800元/吨，那么刘总经理的采购量为多少时，该水果基地在这次买卖中所获得利润最大？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是等差数列，满足， ，数列满足， ，且是等比数列.

    （1）求数列和的通项公式；

    （2）求数列的前项和.

    查看答案和解析>>

    同步练习册答案