【题目】设F为抛物线C：y2=4x的焦点，过点P（﹣1，0）的直线l交抛物线C于两点A，B，点Q为线段AB的中点，若|FQ|=2，则直线l的斜率等于 ．
【答案】不存在
【解析】解：由题意设直线l的方程为my=x+1，联立 
得到y2﹣4my+4=0，△=16m2﹣16=16（m2﹣1）＞0．
设A（x1 ， y1），B（x2 ， y2），Q（x0 ， y0）．
∴y1+y2=4m，∴ 
=2m，∴x0=my0﹣1=2m2﹣1．
∴Q（2m2﹣1，2m），
由抛物线C：y2=4x得焦点F（1，0）．
∵|QF|=2，∴ 
，化为m2=1，解得m=±1，不满足△＞0．
故满足条件的直线l不存在．
所以答案是不存在．
【考点精析】解答此题的关键在于理解直线的斜率的相关知识，掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα．
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中．已知向量 
、 
，| |=| |=1， =0，点Q满足 
= 
（ + ），曲线C={P| 
= cosθ+ sinθ，0≤θ≤2π}，区域Ω={P|0＜r≤| 
|≤R，r＜R}．若C∩Ω为两段分离的曲线，则（ ）
A.1＜r＜R＜3
B.1＜r＜3≤R
C.r≤1＜R＜3
D.1＜r＜3＜R
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从3名骨科、4名脑外科和5名内科医生中选派5人组成一个抗震救灾医疗小组，则骨科、脑外科和内科医生都至少有1人的选派方法种数是（用数字作答）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，过点
且互相垂直的两条直线分别与圆
交于点A，B，与圆
交于点C，D．
(1) 若AB＝
，求CD的长；
(2)若直线
斜率为2，求
的面积；
(3) 若CD的中点为E，求△ABE面积的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取m个作为样本，称出它们的重量（单位：克），重量分组区间为
，
，
，
，由此得到样本的重量频率分布直方图（如图）.
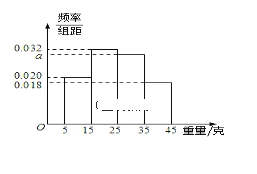
（1）根据样本数据，试估计盒子中小球重量的中位数与平均值（精确到0.01）；
（2）从盒子装的大量小球中，随机抽取3个小球，其中重量在内的小球个数为
，求的分布列和数学期望。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在公差为d的等差数列{an}中，已知a1=10，且a1 ， 2a2+2，5a3成等比数列．
（1）求d，an；
（2）若d＜0，求|a1|+|a2|+|a3|+…+|an|．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一半径为
的水轮如图所示，水轮圆心
距离水面
；已知水轮按逆时针做匀速转动，每
转一圈，如果当水轮上点
从水中浮现时（图中点
）开始计算时间.
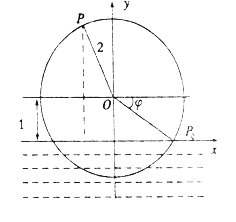
（1）以水轮所在平面与水面的交线为
轴，以过点且与水面垂直的直线为
轴，建立如图所示的直角坐标系，将点
距离水面的高度
表示为时间
的函数；
（2）点第一次到达最高点大约要多长时间？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C： 
（a＞b＞0）的两个焦点分别为F1（﹣1，0），F2（1，0），且椭圆C经过点 
．
（1）求椭圆C的离心率：
（2）设过点A（0，2）的直线l与椭圆C交于M，N两点，点Q是线段MN上的点，且 
，求点Q的轨迹方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
