
| A. | 若σ⊥β,σ∩β=m,n⊥m,则n⊥σ或n⊥β | |
| B. | 若m不垂直于σ,则m不可能垂直于σ内的无数条直线 | |
| C. | 若σ∩β=m,m∥n,且n?σ,n?β,则n∥σ且n∥β | |
| D. | 若σ⊥β,m∥n,n⊥β,则m∥σ |
分析 A.根据面面垂直和直线垂直的性质进行判断,
B.根据线面垂直的定义进行判断,
C.根据线面平行的性质和定义进行判断,
D.根据线面平行和面面垂直的性质进行判断.
解答 解:A.若σ⊥β,σ∩β=m,n⊥m,则n⊥σ或n⊥β或者n与平面相交,或n在平面内,故A错误,
B.若m不垂直于σ,则m有可能垂直于σ内的无数条直线,比如人在上楼梯的过程中,人和楼梯的台阶满足垂直关系,故B错误,
C.若σ∩β=m,m∥n,且n?σ,n?β,则n∥σ且n∥β,正确,
D.若σ⊥β,m∥n,n⊥β,则m∥σ或m?σ,故D错误,
故选:C
点评 本题主要考查与空间直线和平面位置有关的命题的真假判断,根据相应的定义或性质是解决本题的关键.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
| 身高x/cm | 165 | 168 | 170 | 172 | 175 |
| 体重y/kg | 49 | 51 | 55 | 61 | 69 |
| A. | 73kg | B. | 75kg | C. | 77kg | D. | 79kg |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}$ | B. | $-\frac{9}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{7}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
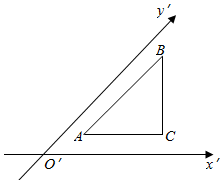
| A. | 4$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | 8$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)为奇函数,值域为$[\frac{1}{2},2]$ | B. | f(x)为偶函数,值域为[1,2] | ||
| C. | f(x)为非奇非偶函数,值域为$[\frac{1}{2},2]$ | D. | f(x)为非奇非偶函数,值域为[1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com