
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 是自然对数的底数)时,不等式
是自然对数的底数)时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)求得![]() 的导数,由
的导数,由![]() 求得切线的斜率,由点斜式方程可得所求切线的方程;(2)由题意可得
求得切线的斜率,由点斜式方程可得所求切线的方程;(2)由题意可得![]() 在
在![]() 恒成立,由
恒成立,由![]() 时,
时,![]() 递增,可得值域为
递增,可得值域为![]() ,运用分离参数,求得右边函数的最小值,注意运用导数,判断单调性,即可得到所求范围.
,运用分离参数,求得右边函数的最小值,注意运用导数,判断单调性,即可得到所求范围.
试题解析:(1)f(x)=4x-![]() 的导数为f′(x)=4+
的导数为f′(x)=4+![]() ,可得在点(2,f(2))处的切线斜率为k=4+1=5,切点为(2,6),可得切线的方程为y-6=5(x-2),即为y=5x-4.
,可得在点(2,f(2))处的切线斜率为k=4+1=5,切点为(2,6),可得切线的方程为y-6=5(x-2),即为y=5x-4.
(2)x∈(1,![]() ]时,不等式f(x)-g(x)<3恒成立,即为m
]时,不等式f(x)-g(x)<3恒成立,即为m![]() <3ln x+3在(1,
<3ln x+3在(1,![]() ]恒成立, 由1<x≤
]恒成立, 由1<x≤![]() 时,3ln x+3∈
时,3ln x+3∈![]() ,x-
,x-![]() 递增,可得值域为
递增,可得值域为![]() ,即有m<
,即有m<![]() 的最小值,
的最小值,
由![]() 的导数为
的导数为![]() ,
,
可得1<x≤![]() 时,h′(x)<0,h(x)递减,可得x=
时,h′(x)<0,h(x)递减,可得x=![]() 时,h(x)取得最小值,且为
时,h(x)取得最小值,且为![]() .
.
可得m<![]() .则m的范围是
.则m的范围是![]() .
.
【方法点晴】本题主要考查利用导数求曲线切线以及利用导数研究函数的单调性、不等式恒成立问题,属于难题.求曲线切线方程的一般步骤是:(1)求出![]() 在
在![]() 处的导数,即
处的导数,即![]() 在点
在点![]()
![]() 出的切线斜率(当曲线
出的切线斜率(当曲线![]() 在
在![]() 处的切线与
处的切线与![]() 轴平行时,在 处导数不存在,切线方程为
轴平行时,在 处导数不存在,切线方程为![]() );(2)由点斜式求得切线方程
);(2)由点斜式求得切线方程![]() .
.


科目:高中数学 来源: 题型:
【题目】已知y=f(x)是偶函数,而y=f(x+1)是奇函数,且对任意0≤x≤1,都有f(x)≥0,f(x)是增函数,则a=f(2010),b=f( ![]() ),c=﹣f(
),c=﹣f( ![]() )的大小关系是( )
)的大小关系是( )
A.b<c<a
B.c<b<a
C.a<c<b
D.a<b<c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的历史收益率的频率分布直方图如图所示:
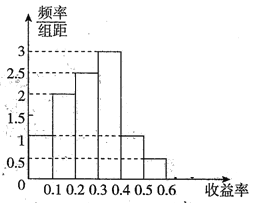
(1)试计算该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万件)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
据此计算出的回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从上述五组销量中随机抽取两组,求两组销量中恰有一组超过6万件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对甲、乙的学习成绩进行抽样分析,各抽五门功课,得到的观测值如表:
甲 | 60 | 80 | 70 | 90 | 70 |
乙 | 80 | 60 | 70 | 80 | 75 |
问:甲、乙谁的平均成绩较好?谁的各门功课发展较平衡?( )
A.甲的平均成绩较好,乙的各门功课发展较平衡
B.甲的平均成绩较好,甲的各门功课发展较平衡
C.乙的平均成绩较好,甲的各门功课发展较平衡
D.乙的平均成绩较好,乙的各门功课发展较平衡
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
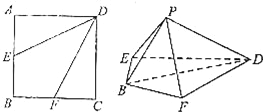
【题目】
如图,在正方形ABCD中,点E,F分别是AB,BC的中点.将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于P.
(1)求证:平面PBD⊥平面BFDE;
(2)求二面角P﹣DE﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ex﹣ ![]() (e为自然对数的底数).
(e为自然对数的底数).
(1)求函数y=f(x)在点(1,f(1))处的切线方程;
(2)当x∈(﹣1,+∞)时,证明:f(x)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某学校组织的一次智力竞赛中,比赛共分为两个环节,其中第一环节竞赛题有A、B两组题,每个选手最多有3次答题机会,答对一道A组题得20分,答对一道B组题得30分.选手可以任意选择答题的顺序,如果前两次得分之和超过30分即停止答题,进入下一环节比赛,否则答3次.某同学正确回答A组题的概率都是p,正确回答B组题的概率都是 ![]() ,且回答正确与否相互之间没有影响.该同学选择先答一道B组题,然后都答A组题.已知第一环节比赛结束时该同学得分超过30分的概率为
,且回答正确与否相互之间没有影响.该同学选择先答一道B组题,然后都答A组题.已知第一环节比赛结束时该同学得分超过30分的概率为 ![]() .
.
(1)求p的值;
(2)用ξ表示第一环节比赛结束后该同学的总得分,求随机变量ξ的数学期望;
(3)试比较该同学选择都回答A组题与选择上述方式答题,能进入下一环节竞赛的概率的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com