
| A. | [$\frac{3}{16},\frac{21}{80}$] | B. | [$\frac{3}{8},\frac{21}{40}$] | C. | [$\frac{3}{4},\frac{21}{20}$] | D. | [$\frac{3}{2},\frac{21}{10}$] |
分析 根据f(-x0)+f(x0)=1,代入函数值整理成${{(2}^{{-x}_{0}}{+2}^{{x}_{0}})}^{2}$-4m(${2}^{{-x}_{0}}$+${2}^{{x}_{0}}$)-1=0,设${2}^{{-x}_{0}}$+${2}^{{x}_{0}}$=t,$\frac{5}{2}$≥t≥2,得出t2-4mt-1=0;分离参数m,利用函数的单调性求出m的取值范围.
解答 解:∵函数f(x)=m•2x+2-4x,且存在实数x0∈[-1,1],使f(-x0)+f(x0)=1,
∴4m•${2}^{{-x}_{0}}$-${4}^{{-x}_{0}}$+4m•${2}^{{x}_{0}}$-${4}^{{x}_{0}}$=1;
整理成${{(2}^{{-x}_{0}}{+2}^{{x}_{0}})}^{2}$-4m(${2}^{{-x}_{0}}$+${2}^{{x}_{0}}$)-1=0,
设${2}^{{-x}_{0}}$+${2}^{{x}_{0}}$=t,其中$\frac{5}{2}$≥t≥2;
∴t2-4mt-1=0;
分离参数m=$\frac{1}{4}$(t-$\frac{1}{t}$),根据单调性的定义知该函数在[2,$\frac{5}{2}$]上是增函数;
∴m≥$\frac{1}{4}$×(2-$\frac{1}{2}$)=$\frac{3}{8}$,
且m≤$\frac{1}{4}$×($\frac{5}{2}$-$\frac{2}{5}$)=$\frac{21}{40}$;
∴实数m的取值范围是[$\frac{3}{8}$,$\frac{21}{40}$].
故选:B.
点评 本题考查完了全平方式、换元法以及基本不等式的应用问题,也考查了函数的单调性问题,是综合性题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
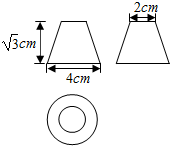
| A. | $\frac{{7\sqrt{3}π}}{3}$ | B. | $\frac{{8\sqrt{3}π}}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com