
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=2,AA′=1,点M,N分别为A′B和B′C′的中点.
如图,直三棱柱ABC-A′B′C′,∠BAC=90°,AB=AC=2,AA′=1,点M,N分别为A′B和B′C′的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
已知抛物线 的焦点为
的焦点为 ,过点
,过点 的直线交抛物线于
的直线交抛物线于 两点.
两点.
(1)若 ,求直线
,求直线 的斜率;
的斜率;
(2)设点 在线段
在线段 上运动,原点
上运动,原点 关于点
关于点 的对称点为
的对称点为 ,求四边形
,求四边形 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年重庆市高二上学期入学考试数学试卷(解析版) 题型:解答题
已知数列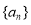 满足
满足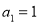 ,
,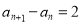 ,等比数列
,等比数列 满足
满足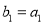 ,
, .
.
(I)求数列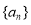 、
、 的通项公式;
的通项公式;
(II)设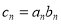 ,求数列
,求数列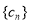 的前
的前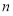 项和
项和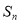 .
.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:解答题
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点.
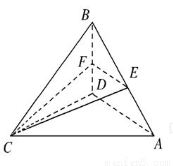
求证:(1)直线EF∥面ACD;
(2)平面EFC⊥平面BCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com