
分析 (1)由已知中函数f(x)=$\frac{ax+b}{{x}^{2}+1}$是定义在(-1,1)上的奇函数,且f($\frac{1}{2}$)=$\frac{2}{5}$.求出a,b的值,进而可得:函数f(x)的解析式;
(2)f(x)在(-1,1)上为增函数,
证法一:设-1<x1<x2<1,作差可得f(x1)<f(x2),根据函数单调性的定义,可得:f(x)在在(-1,1)上为增函数,
证法二:求导,根据当x∈(-1,1)时,f′(x)>0恒成立,可得:f(x)在在(-1,1)上为增函数,
(3)根据函数的奇偶性和单调性,可将不等式f(2x-1)+f(x)<0化为-1<2x-1<-x<1,解得答案.
解答 解:(1)∵函数f(x)=$\frac{ax+b}{{x}^{2}+1}$是定义在(-1,1)上的奇函数,
∴f(0)=0,
又∵f($\frac{1}{2}$)=$\frac{2}{5}$.
∴b=0,a=1,
∴f(x)=$\frac{x}{{x}^{2}+1}$.
(2)f(x)在(-1,1)上为增函数,理由如下:
证法一:设-1<x1<x2<1,
则1-x1•x2>0,x1-x2>0,1+x12>0,1+x22>0,
∴f(x1)-f(x2)=$\frac{{x}_{1}}{{{x}_{1}}^{2}+1}$-$\frac{{x}_{2}}{{{x}_{2}}^{2}+1}$=$\frac{({x}_{1}-{x}_{2})({1-{x}_{1}x}_{2})}{{{(x}_{1}}^{2}+1){{(x}_{2}}^{2}+1)}$<0,
∴f(x1)<f(x2)
∴f(x)在在(-1,1)上为增函数,
证法二:∵f(x)=$\frac{x}{{x}^{2}+1}$.
∴f′(x)=$\frac{1-{x}^{2}}{{(x}^{2}+1)^{2}}$.
当x∈(-1,1)时,f′(x)>0恒成立,
∴f(x)在在(-1,1)上为增函数,
(3)∵f(2x-1)+f(x)<0,
∴f(2x-1)<-f(x)=f(-x),
又f(x)在在(-1,1)上为递增的奇函数,
∴-1<2x-1<-x<1,
∴0<x<$\frac{1}{3}$,
∴不等式f(2x-1)+f(x)<0的解集为(0,$\frac{1}{3}$).
点评 本题考查的知识点是函数的单调性,函数的奇偶性,函数解析式的求法,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
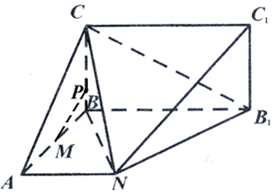 如图,已知平面ABB1N⊥平面BB1C1C,四边形BB1C1C,是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.
如图,已知平面ABB1N⊥平面BB1C1C,四边形BB1C1C,是矩形,ABB1N是梯形,且AN⊥AB,AN∥BB1,AB=BC=AN=4,BB1=8.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com