
分析 求出f(x)在[$\frac{1}{3}$,3]上的解析式,根据f(a)=f(b)得出a,b的关系和b的范围,从而得出ab关于b的表达式,利用b的范围求出ab的范围.
解答 解:设x∈[$\frac{1}{3}$,1],则$\frac{1}{x}$∈[1,3],
∴f(x)=2f($\frac{1}{x}$)=2ln$\frac{1}{x}$,
∴f(x)=$\left\{\begin{array}{l}{2ln\frac{1}{x},\frac{1}{3}≤x≤1}\\{lnx,1<x≤3}\end{array}\right.$.
∴f(x)在[$\frac{1}{3}$,1]上单调递减,在[1,3]上单调递增,
且f($\frac{1}{3}$)=2ln3,f(1)=0,f(3)=ln3,
∵在区间[$\frac{1}{3}$,3]内,存在互不相等的实数a,b使f(a)=f(b),不妨设a<b,
则1<b≤3,2ln$\frac{1}{a}$=lnb,∴$\frac{1}{{a}^{2}}$=b,即a=$\sqrt{\frac{1}{b}}$,
∴ab=$\sqrt{\frac{1}{b}}$•b=$\sqrt{b}$,
∴ab的取值范围是(1,$\sqrt{3}$].
故答案为:$(1,\sqrt{3}]$.
点评 本题考查了函数解析式的求法,函数单调性的判断,函数值域的计算,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
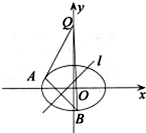 如图,圆O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,圆O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com