
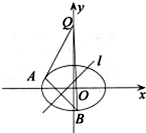
 如图,圆O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.
如图,圆O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于E.分析 (Ⅰ)证明△BDC∽△CDE,即可证明:DC2=DE•DB;
(Ⅱ)连结OD,OD⊥AC,设垂足为F,求出$OF=\frac{1}{3}r\;\;,\;\;DF=\frac{2}{3}r$,利用勾股定理建立方程,即可得出结论.
解答 (Ⅰ)证明:∵D是$\widehat{AC}$的中点,∴∠ABD=∠CBD
又∵∠ABD=∠ACD
∴∠CBD=∠ACD,∠BDC=∠CDE,
∴△BDC∽△CDE,
∴$\frac{BD}{CD}=\frac{DC}{DE}$,即DC2=DE•DB,…(5分)
(Ⅱ)解:连结OD,
∵D是$\widehat{AC}$的中点,
∴OD⊥AC,设垂足为F,
则$OF=\frac{1}{2}DF\;\;,\;\;OF+DF=OD=r$,
∴$OF=\frac{1}{3}r\;\;,\;\;DF=\frac{2}{3}r$,
在Rt△OFC中,OF2+FC2=r2,∴$F{C^2}=\frac{8}{9}{r^2}$,
在Rt△DFC中,DF2+FC2=CD2=48,即${({\frac{2}{3}r})^2}+\frac{8}{9}{r^2}=48$,
得r=6.…(10分)
点评 本题考查三角形相似的判定与性质的运用,考查勾股定理的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com