
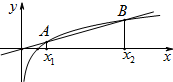
 如图,过原点斜率为k的直线与曲线y=lnx交于两点A(x1,y1),B(x2,y2)
如图,过原点斜率为k的直线与曲线y=lnx交于两点A(x1,y1),B(x2,y2)| A. | ① | B. | ①② | C. | ①③ | D. | ②③ |
分析 构造函数f(x)=kx-lnx,求导可得f′(x)=k-$\frac{1}{x}$,由已知f(x)有两个不同的零点,得k>0,进一步可得f(x)在(0,$\frac{1}{k}$)上单调递减,在($\frac{1}{k},+∞$)上单调递增,画图可得f($\frac{1}{k}$)=1-$ln\frac{1}{k}$<0,则0$<k<\frac{1}{e}$,故①正确;由${x}_{1}<\frac{1}{k}<{x}_{2}$,得$\frac{1}{{x}_{2}}<k<\frac{1}{{x}_{1}}$,故②错误;由图可知,当x∈(x1,x2)时,f(x)=kx-lnx先减后增且恒为负,故③正确.
解答 解:令f(x)=kx-lnx,则f′(x)=k-$\frac{1}{x}$,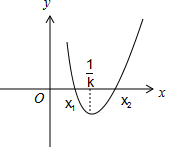
由已知f(x)有两个不同的零点,则k>0,
∴f(x)在(0,$\frac{1}{k}$)上单调递减,在($\frac{1}{k},+∞$)上单调递增,
∴f($\frac{1}{k}$)=1-$ln\frac{1}{k}$<0,则0$<k<\frac{1}{e}$,故①正确;
且有${x}_{1}<\frac{1}{k}<{x}_{2}$,∴$\frac{1}{{x}_{2}}<k<\frac{1}{{x}_{1}}$,故②错误;
当x∈(x1,x2)时,f(x)=kx-lnx先减后增且恒为负,故③正确.
∴所有正确结论的序号是①③.
故选:C.
点评 本题考查命题的真假判断与应用,考查了利用导数研究函数的单调性,考查数形结合的解题思想方法,是中档题.


科目:高中数学 来源: 题型:填空题
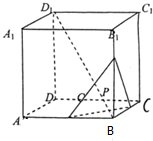 如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):
如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1≤m≤1 | B. | m≤1 | C. | -2≤m≤2 | D. | m≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e2f(-2)>f(0),f(2)>e2f(0) | B. | e2f(-2)<f(0),f(2)<e2f(0) | ||
| C. | e2f(-2)>f(0),f(2)<e2f(0) | D. | e2f(-2)<f(0),f(2)>e2f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b=($\sqrt{2}$-1)a | B. | b=($\sqrt{2}$+1)a | C. | b=$\frac{2-\sqrt{2}}{2}$a | D. | b=$\frac{2+\sqrt{2}}{2}$a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | 6$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com