
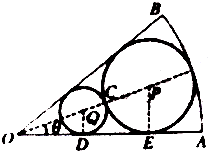
 如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.
如图,在半径为1、圆心角为变量2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两半径相切并与圆P外切的小圆Q,设圆P的半径为R,圆Q的半径为r.分析 (1)在直角三角形OEP中$OP=\frac{PE}{sinθ}=\frac{R}{sinθ}$,即可用θ表示圆P的半径R;
(2)令sinθ=t,0<t<1,利用导数的性质能求出圆Q的半径的最大值.
解答 解:(1)如图,在直角三角形OEP中$OP=\frac{PE}{sinθ}=\frac{R}{sinθ}$…2分
因为半径为1,所以OP+R=1,所以$R=\frac{sinθ}{1+sinθ}$…5分
(2)在直角三角形ODQ,OQ=$\frac{DQ}{sinθ}$=$\frac{r}{sinθ}$,OQ+r+2R=1,
∴$r=\frac{sinθ(1-sinθ)}{{{{(1+sinθ)}^2}}}$…10分
令$sinθ=t,(0<t<1),r=\frac{{t-{t^2}}}{{{{(1+t)}^2}}},r'=\frac{1-3t}{{{{(1+t)}^3}}}$
令$r'=0,t=\frac{1}{3}$$0<t<\frac{1}{3},r'>0;\frac{1}{3}<t<1,r'<0$
所以$t=\frac{1}{3}$时,$r=\frac{1}{8}$…14分
答:存在θ为锐角,当$sinθ=\frac{1}{3}$时,圆Q半径得最大值$\frac{1}{8}$.…15分.
点评 本题考查函数的求法,考查圆的半径的最大值的求法,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | A${\;}_{6}^{6}$ | B. | 2A${\;}_{3}^{3}$ | C. | A${\;}_{3}^{3}$A${\;}_{3}^{3}$ | D. | $A_3^3A_4^4$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,2014] | B. | [-1,1)∪(1,2014] | C. | (1,2015] | D. | [0,1)∪(1,2014] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等边三角形 | B. | 腰长为a的等腰三角形 | ||
| C. | 底边长为a的等腰三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com