
分析 |x-1|+|2x+2|=$\left\{\begin{array}{l}{3x+1,x≥1}\\{x+3,-1<x<1}\\{-3x-1,x≤-1}\end{array}\right.$,利用一次函数的单调性可得最小值为:2.不等式|x-1|+|2x+2|≥a2+$\frac{1}{2}$a+2转化为:2≥a2+$\frac{1}{2}$a+2,解出即可得出.
解答 解:∵|x-1|+|2x+2|=$\left\{\begin{array}{l}{3x+1,x≥1}\\{x+3,-1<x<1}\\{-3x-1,x≤-1}\end{array}\right.$,可得最小值为:2.
∴不等式|x-1|+|2x+2|≥a2+$\frac{1}{2}$a+2转化为:2≥a2+$\frac{1}{2}$a+2,解得$-\frac{1}{2}≤a≤0$.
∴实数a的取值范围是$[-\frac{1}{2},0]$.
故答案为:$[-\frac{1}{2},0]$.
点评 本题考查了绝对值不等式的解法、一元二次不等式的解法,考查了推理能力与计算能力,属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $100\sqrt{3}$ | B. | $100\sqrt{6}$ | C. | 100 | D. | $100\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
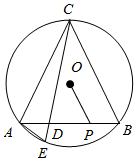 如图,已知AB是⊙O的弦,P是AB上一点.
如图,已知AB是⊙O的弦,P是AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
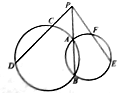 如图,两圆相交于A,B两点,P为BA延长线上任意一点,从P引两圆的割线PCD,PFE.
如图,两圆相交于A,B两点,P为BA延长线上任意一点,从P引两圆的割线PCD,PFE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
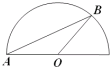 如图所示,OA=1,在以O为圆心,以OA为半径的半圆弧上随机取一点B,则△AOB的面积小于$\frac{1}{4}$的概率为( )
如图所示,OA=1,在以O为圆心,以OA为半径的半圆弧上随机取一点B,则△AOB的面积小于$\frac{1}{4}$的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 数学成绩 物理成绩 | 优秀 | 不优秀 | 合计 |
| 优秀 | 5 | 2 | 7 |
| 不优秀 | 1 | 12 | 13 |
| 合计 | 6 | 14 | 20 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 班级 | 优秀 | 非优秀 | 合计 |
| 甲班 | 18 | ||
| 乙班 | 43 | ||
| 合计 | 110 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com