
已知函数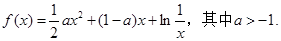
(Ⅰ)若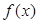 有两个极值点,求实数
有两个极值点,求实数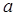 的取值范围;
的取值范围;
(Ⅱ)当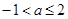 时,讨论函数
时,讨论函数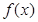 的零点个数.
的零点个数.
(Ⅰ)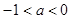 。
。
(Ⅱ)综上可知,当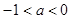 或
或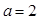 时,函数
时,函数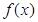 有且仅有一个零点;当
有且仅有一个零点;当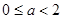 时,函数
时,函数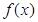 无零点.
无零点.
【解析】
试题分析:(Ⅰ)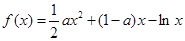 ,
,
法1: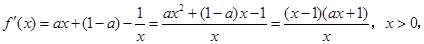
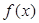 有两个极值点等价于方程
有两个极值点等价于方程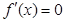 在
在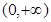 上有两个不等的实根,等价于
上有两个不等的实根,等价于
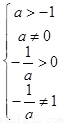 ,解得
,解得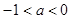 ,即为所求的实数
,即为所求的实数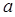 的取值范围.
的取值范围.
法2: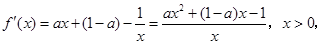
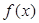 有两个极值点等价于方程
有两个极值点等价于方程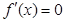 在
在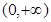 上有两个不等的实根,即方程
上有两个不等的实根,即方程
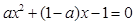 在
在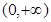 上有两个不等的实根,等价于
上有两个不等的实根,等价于
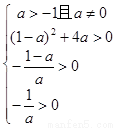 ,
,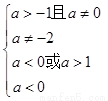 ,解得
,解得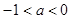 ,即为所求的实数
,即为所求的实数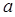 的取值范围.
的取值范围.
法3:
,即方程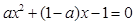 在
在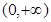 上有两个不等的实根,令
上有两个不等的实根,令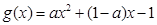 ,则其图象对称轴为直线
,则其图象对称轴为直线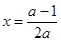 ,图象恒过
,图象恒过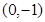 点,
点,
问题条件等价于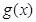 的图象与
的图象与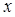 轴正半轴有两个不同的交点,等价于
轴正半轴有两个不同的交点,等价于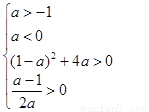 ,
,
(Ⅱ)法1:(1)当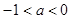 时,
时,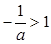 ,
,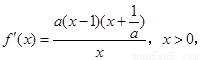
由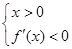 得,
得,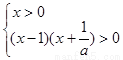 ,解得
,解得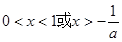 ,
,
由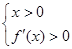 得,
得, ,解得
,解得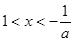 ,
,
从而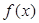 在
在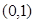 、
、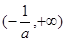 上递减,在
上递减,在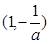 上递增,
上递增,
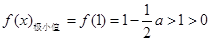 ,
,
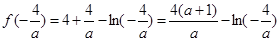 ,因为
,因为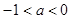 ,所以
,所以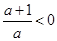 ,又
,又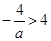 ,所以
,所以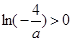 ,从而
,从而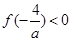 .
.
又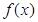 的图象连续不断,故当
的图象连续不断,故当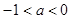 时,
时,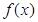 的图象与
的图象与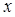 轴有且仅有一个交点.
轴有且仅有一个交点.
法2:
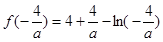 ,令
,令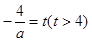 ,考察函数
,考察函数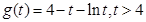 ,由于
,由于 ,所以
,所以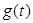 在
在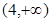 上递减,
上递减,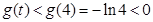 ,即
,即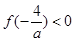 ,
,
(2)当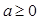 时,因为
时,因为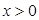 ,所以
,所以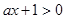 ,则当
,则当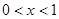 时,
时,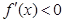 ;当
;当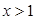 时,
时,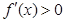 .从而
.从而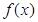 在
在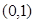 上递减,在
上递减,在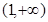 上递增,
上递增,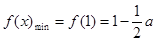 .
.
①若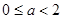 ,则
,则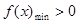 ,此时
,此时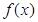 的图象与
的图象与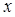 轴无交点.
轴无交点.
②若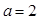 ,则
,则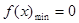 ,
,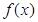 的图象与
的图象与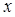 轴有且仅有一个交点.
轴有且仅有一个交点.
综上可知,当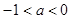 或
或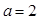 时,函数
时,函数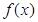 有且仅有一个零点;当
有且仅有一个零点;当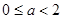 时,函数
时,函数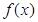 无零点.
无零点.
考点:应用导数研究函数的单调性、极值、图象特征、函数的零点,不等式组的解法。
点评:典型题,本题解答思路明确,注意是应用导数研究函数的单调性、极值、图象特征、函数的零点等。解答(I)时关键之一是认识到“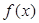 有两个极值点等价于方程
有两个极值点等价于方程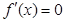 在
在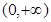 上有两个不等的实根”。解答(II)时,通过研究函数的单调性、极值等,明确了函数图像的大致形态,又通过讨论a 的不同取值范围,确定出函数零点的个数。解法较多,对启迪学生的思维很有帮助。
上有两个不等的实根”。解答(II)时,通过研究函数的单调性、极值等,明确了函数图像的大致形态,又通过讨论a 的不同取值范围,确定出函数零点的个数。解法较多,对启迪学生的思维很有帮助。


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
(12分)已知函数![]()
(1)若![]() 有极值,求b的取值范围;
有极值,求b的取值范围;
(2) 若![]() 在
在![]() 处取得极值时,当
处取得极值时,当![]() 恒成立,求c的取值范围;
恒成立,求c的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数![]()
(1)若![]() 有极值,求b的取值范围;
有极值,求b的取值范围;
(2)若![]() 在
在![]() 处取得极值时,当
处取得极值时,当![]() 恒成立,求c的取值范围;
恒成立,求c的取值范围;
(3)若![]() 在
在![]() 处取得极值时,证明:对[-1,2]内的任意两个值
处取得极值时,证明:对[-1,2]内的任意两个值![]() 都有
都有![]() .
.
查看答案和解析>>
科目:高中数学 来源:江苏省启东中学2010年高三适应性考试 题型:解答题
已知函数 .
.
(Ⅰ)若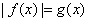 有两个不同的解,求
有两个不同的解,求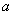 的值;
的值;
(Ⅱ)若当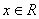 时,不等式
时,不等式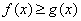 恒成立,求
恒成立,求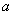 的取值范围;
的取值范围;
(Ⅲ)求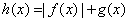 在
在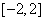 上的最大值.
上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com