
分析 确定直线过定点(3,0),可得F的坐标,由双曲线的定义,再根据点P在双曲线的右支上,可得|PF2|≥c-a,从而a的取值范围.
解答 解:设点A,B的坐标分别为(x1,y1),(x2,y2),
设直线方程为x=my+b,
联立方程,消去x得y2-3my-3b=0,
则y1y2=-3b,x1x2=b2,
又$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则x1x2+y1y2=0,
即-3b+b2=0,
解得b=0(舍去)或b=3,
故直线过定点(3,0),
∴F(3,0),
∵|$\overrightarrow{PF′}$|=2|$\overrightarrow{PF}$|,
∴由双曲线的定义可得|$\overrightarrow{PF′}$|-|$\overrightarrow{PF}$|=|$\overrightarrow{PF}$|=2a,
∵点P在双曲线的右支上,
∴|PF|≥c-a,
∴2a≥c-a,∴a≥1,
∵$\frac{c}{a}>1$,∴a<3,
∴a的取值范围是[1,3),
故答案为[1,3).
点评 本题考查向量垂直的条件,同时考查直线与抛物线的位置关系,以及证明直线恒过定点,双曲线的简单性质的应用,考查学生的计算能力,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
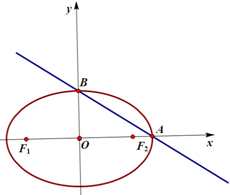 椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.
椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\overrightarrow{OP}$ | B. | $3\overrightarrow{OP}$ | C. | $2\overrightarrow{OP}$ | D. | $\overrightarrow{OP}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com