
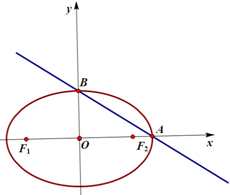
 椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.
椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.分析 (Ⅰ)椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{1}{2}$,整理得:3a2=4b2,由三角形OAB的面积公式可知:$\frac{1}{2}ab=\frac{1}{2}×\frac{{2\sqrt{21}}}{7}\sqrt{{a^2}+{b^2}}$,代入即可求得a和b的值,即可求得椭圆方程;
(Ⅱ)当直线l斜率不存在时,求得t=±$\frac{\sqrt{3}}{2}$,?当直线l斜率存在时,设直线l的方程为y=kx+t,代入椭圆方程,$\overrightarrow{PN}=3\overline{NQ}$,则x1=-3x2,代入上式可得${x_1}=\frac{-12kt}{{4{k^2}+3}}$,${x_2}=\frac{4kt}{{4{k^2}+3}}$,
求得:${k^2}=\frac{{9-3{t^2}}}{{16{t^2}-12}}$,则$\frac{{{t^2}({3-{t^2}})}}{{4{t^2}-3}}>0$,即可求得t的取值范围,由△AON的周长$l=2+|t|+\sqrt{{t^2}+4}$,$t∈({-\sqrt{3}}\right.,\left.{-\frac{{\sqrt{3}}}{2}}]∪[{\frac{{\sqrt{3}}}{2}}\right.,\left.{\sqrt{3}})$是偶函数,由t的取值范围,即可求得△AON周长的取值范围.
解答 解:(Ⅰ)由椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)焦点在x轴上,
∵椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{1}{2}$,整理得:3a2=4b2,…(1分)
又∵坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$.
由三角形OAB的面积公式可知:$\frac{1}{2}ab=\frac{1}{2}×\frac{{2\sqrt{21}}}{7}\sqrt{{a^2}+{b^2}}$,…(2分)
∴$\frac{{\sqrt{3}}}{2}{a^2}=\frac{{2\sqrt{21}}}{7}\sqrt{{a^2}+\frac{3}{4}{a^2}}$,a=2,$b=\sqrt{3}$,
椭圆C的方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1$;…(4分)
(Ⅱ)?当直线l斜率不存在时,
∵经过点N(0,t)的直线l与椭圆C交于不同的两点P,Q,且,$\overrightarrow{PN}=3\overline{NQ}$.
∴$点N为椭圆短轴的四等分点,t=±\frac{{\sqrt{3}}}{2}$,…(5分)
?当直线l斜率存在时,设直线l的方程为y=kx+t,
又设直线l与椭圆C的交点P(x1,y1),Q(x2,y2).
∴$由\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=kx+t\end{array}\right.得(4{k^2}+3){x^2}+8ktx+4{t^2}-12=0$,
∴△>0,即4k2-t2+3>0,(*)
${x_1}+{x_2}=-\frac{8kt}{{4{k^2}+3}}$,${x_1}{x_2}=\frac{{4{t^2}-12}}{{4{k^2}+3}}$…(7分)
又∵$\overrightarrow{PN}=3\overline{NQ}$,
∴x1=-3x2,代入上式可得${x_1}=\frac{-12kt}{{4{k^2}+3}}$,${x_2}=\frac{4kt}{{4{k^2}+3}}$$\frac{-12kt}{{4{k^2}+3}}•\frac{4kt}{{4{k^2}+3}}=\frac{{4{t^2}-12}}{{4{k^2}+3}}$,
化简得:16k2t2+3t2-12k2-9=0,
∴${k^2}=\frac{{9-3{t^2}}}{{16{t^2}-12}}$带入(*)得$\frac{{{t^2}({3-{t^2}})}}{{4{t^2}-3}}>0$,
即又t≠0,
∴(3-t2)(4t2-3)>0
解得;$-\sqrt{3}<t<-\frac{{\sqrt{3}}}{2}或\frac{{\sqrt{3}}}{2}<t<\sqrt{3}$,…(9分)
综上所述实数t的取值范围为:$({-\sqrt{3}}\right.,\left.{-\frac{{\sqrt{3}}}{2}}]∪[{\frac{{\sqrt{3}}}{2}}\right.,\left.{\sqrt{3}})$,…(10分)
又△AON的周长$l=2+|t|+\sqrt{{t^2}+4}$,$t∈({-\sqrt{3}}\right.,\left.{-\frac{{\sqrt{3}}}{2}}]∪[{\frac{{\sqrt{3}}}{2}}\right.,\left.{\sqrt{3}})$是偶函数.
∴当$t∈[{\frac{{\sqrt{3}}}{2}}\right.,\left.{\sqrt{3}})$时,$l=2+t+\sqrt{{t^2}+4}$在$[{\frac{{\sqrt{3}}}{2}}\right.,\left.{\sqrt{3}})$上单调递增,
∴$l∈[{2+\frac{{\sqrt{3}}}{2}}\right.+\frac{{\sqrt{19}}}{2},\left.{2+\sqrt{3}+\sqrt{7}})$,
∴△AON周长的取值范围为[2+$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{19}}{2}$,2+$\sqrt{3}$+$\sqrt{7}$).…(12分)
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理及函数单调性的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}$+$\frac{y^2}{5}$=1(y≠0) | B. | $\frac{y^2}{9}$+$\frac{x^2}{5}$=1(x≠0) | C. | $\frac{x^2}{9}$+$\frac{y^2}{5}$=1(x≠3) | D. | $\frac{y^2}{9}$+$\frac{x^2}{5}$=1(y≠3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 减少3.5个单位 | B. | 增加2个单位 | C. | 增加3.5个单位 | D. | 减少2个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com