
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 ρ=2cosθ+4sinθ化为普通方程,将直线的参数方程化为标准形式,利用弦心距半径半弦长满足的勾股定理,即可求弦长.
解答 解:圆C的极坐标方程为ρ=2cosθ+4sinθ化为直角坐标方程为x2+y2-2x-4y=0,圆的圆心坐标(1,2),半径为$\sqrt{5}$.
直线l的参数方程是$\left\{\begin{array}{l}{x=1+\frac{1}{2}t}\\{y=\frac{\sqrt{3}}{2}t}\end{array}\right.$(t为参数),化为$\sqrt{3}$x-y-$\sqrt{3}$=0,
圆心到直线的距离为:d=$\frac{2}{\sqrt{3+1}}$=1
∴曲线C被直线l截得的弦长为2$\sqrt{5-1}$=4.
故选D.
点评 本题考查参数方程化为标准方程,极坐标方程化为直角坐标方程,考查学生的计算能力,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{7}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
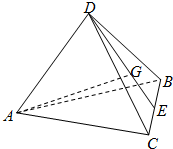 如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.
如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
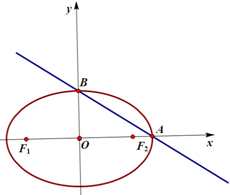 椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.
椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com