
分析 (1)求出函数的导数,利用函数的极值点,列出方程组即可求出a,b的值;
(2)利用导函数,判断函数的单调性,然后求解极值以及端点值,即可得到函数的最值.
解答 解:(1)f′(x)=6x2+6ax+3b,
因为函数f(x)在x=1 及x=2 取得极值,
则有f′(1)=0,f′(2)=0.
即 $\left\{\begin{array}{l}{6+6a+3b=0}\\{24+12a+3b=0}\end{array}\right.$
解得a=-3,b=4.….4分
(2)由(1)可知f(x)=2x3-9x2+12x+8c,
f′(x)=6x2-18x+12=6(x-1)(x-2).
当x∈(0,1)时,f′(x)>0;
当x∈(1,2)时,f′(x)<0;
当x∈(2,3)时,f′(x)>0…6分
则当x∈[0,3]时,f(x)的最大值为f(3)=9+8c…8分
最小值为f(0)=8c,最大值为f(3)=8c…10分
点评 本题考查函数的导数的综合应用,考查转化思想以及计算能力.


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
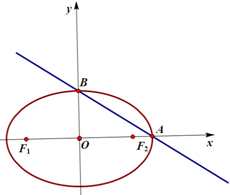 椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.
椭圆C;$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别是F1,F2,右顶点为A,上顶点为B,坐标系原点O到直线AB的距离为$\frac{{2\sqrt{21}}}{7}$,椭圆的离心率是$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com