
| A. | (3,-$\frac{9}{8}$) | B. | (3,-$\frac{7}{8}$) | C. | (5,-$\frac{9}{8}$) | D. | (4,-$\frac{5}{8}$) |
分析 根据题意可得PA+BN的最小值为EF,此时,1≤a≤3,且这3个点共线,故有ME、EF的斜率相等,求得a的值,可得A、P、N三点的坐标,则PN、PA的中垂线的交点坐标,即为所求.
解答 解:由于AB、PN的长度为定值,故只要PA+BN最小即可.
由于PA+BN=$\sqrt{{(a-1)}^{2}+9}$+$\sqrt{{(a-3)}^{2}+1}$,表示动点M(a,0)到E(1,3)、F(3,-1)的距离之和,
故PA+BN的最小值为EF,此时,1≤a≤3,且这3个点共线,故有ME、EF的斜率相等,
即$\frac{0-3}{a-1}$=$\frac{0+1}{a-3}$,a=$\frac{5}{2}$,此时,A(1,-2),P($\frac{5}{2}$,1),N($\frac{7}{2}$,1).
此时,PN的中垂线方程为x=3,PA的中垂线方程为y+$\frac{1}{2}$=-$\frac{1}{2}$(x-$\frac{7}{4}$),
这两条中垂线的交点为(3,-$\frac{9}{8}$),
即为过三点A,P,N的圆的圆心坐标,
故选:A.
点评 本题主要考查两点间的距离公式,三点共线的性质、圆心的性质,属于中档题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ | B. | $?m∈[{0,1}],x+\frac{1}{x}≥{2^m}$ | C. | $?m∈[{0,1}],x+\frac{1}{x}≤{2^m}$ | D. | $?m∈[{0,1}],x+\frac{1}{x}<{2^m}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$| | B. | $\frac{1}{2}$$|\begin{array}{l}{{x}_{1}}&{{y}_{1}}&{1}\\{{x}_{2}}&{{y}_{2}}&{1}\\{{x}_{3}}&{{y}_{3}}&{1}\end{array}|$ | ||
| C. | $\frac{1}{2}$|$\overrightarrow{AB}$$•\overrightarrow{AC}$| | D. | $\frac{1}{2}$(cos|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
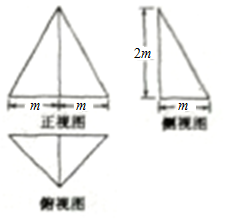 一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )
一个几何体的正视图、侧视图和俯视图如图所示,若这个几何体的外接球的表面积为100π,则该几何体的体积为( )| A. | $36\sqrt{3}$ | B. | $\frac{98}{3}$ | C. | $\frac{116}{3}$ | D. | $\frac{128}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com