
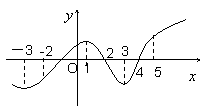
如图是函数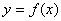 的导函数
的导函数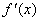 的图象,则下面判断正确的是( ).
的图象,则下面判断正确的是( ).
 A.函数
A.函数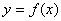 在区间
在区间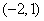 上单调递增
上单调递增
B.函数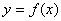 在
在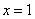 处取得极大值
处取得极大值
C.函数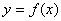 在
在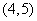 上单调递增
上单调递增
D.当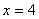 时,
时,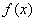 取极大值
取极大值
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
已知抛物线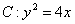 的焦点为
的焦点为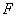 .
.
(Ⅰ)点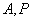 满足
满足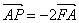 .当点
.当点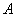 在抛物线
在抛物线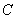 上运动时,求动点
上运动时,求动点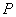 的轨迹方程;
的轨迹方程;
(Ⅱ)设斜率为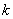 的直线
的直线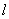 过定点
过定点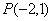 ,求直线
,求直线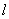 与抛物线
与抛物线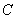 恰好有一个公共点、两个公共点、没有公共点时
恰好有一个公共点、两个公共点、没有公共点时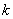 的相应取值范围.
的相应取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法中,正确的是( )
A.“明天降雨的概率是80%”表示明天有80%的时间降雨
B.“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上
C.“彩票中奖的概率是1%”表示买100张彩票一定有1张会中奖
D.在同一年出生的367名学生中,至少有两人的生日是同一天
查看答案和解析>>
科目:高中数学 来源: 题型:
为了保护环境,某工厂在政府部门的鼓励下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本 (万元)与处理量
(万元)与处理量 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为:
 ,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(1)当 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不会亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少?并求出该最少处理成本.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com