
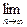 S2n<3,求q的取值范围
S2n<3,求q的取值范围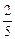
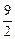 ,
,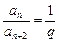 ,即an+2=q·an
,即an+2=q·an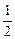 qn(n=1,2,3,…)
qn(n=1,2,3,…)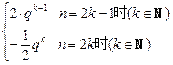
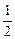 qk,则n=2k+2时,由于a2k+2=q·a2k?,
qk,则n=2k+2时,由于a2k+2=q·a2k?,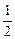 qk+1,这说明n=2k成立,可推知n=2k+2也成立.
qk+1,这说明n=2k成立,可推知n=2k+2也成立.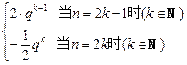
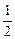 (q+q2+…+qn)
(q+q2+…+qn)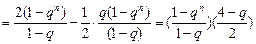
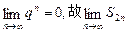 =
=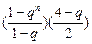
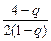 <3,并注意1-q>0,|q|<1解得-1<q<0或0<q<
<3,并注意1-q>0,|q|<1解得-1<q<0或0<q<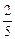


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com