练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
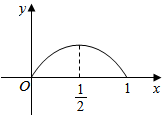
    10．点P从点O出发，按逆时针方向沿周长为l的图形运动一周，O，P两点连线的距离y与点P走过的路程x的函数关系如图，那么点P所走的图形是（　　）
    A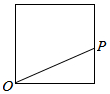．B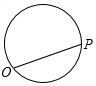．C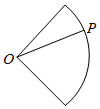．D．

    分析 根据O，P两点连线的距离y与点P走过的路程x的函数图象，由图象可知函数值随自变量的变化成轴对称性并且变化圆滑．由此即可排除A、C．D．

    解答 解：观察函数的运动图象，可以发现两个显著特点：
    ①点P运动到周长的一半时，OP最大；
    ②点P的运动图象是抛物线．
    设点M为周长的一半，
    A．当点P在线段OA上运动时，y=x，其图象是一条线段，不符合条件，

    B．满足条件．

    C．当点P在线段OA上运动时，y=x，其图象是一条线段，不符合条件，

    D．OM≤OP，不符合条件①，并且OP的距离不是对称变化的，因此排除选项D．

    故选：B．

    点评 本题考查函数图象的识别和判断，考查对于运动问题的深刻理解，解题关键是认真分析函数图象的特点．考查学生分析问题的能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．函数f（x）=x2+ax+b，其中a∈R，b∈R且（b+4）2-a2=4，已知对任意的x∈R不等式f（x）≥-2恒成立．
    （1）求实数a，b的值；
    （2）若函数g（x）=$\left\{\begin{array}{l}{f（x）+x+4，x＜f（x）}\\{f（x）-x，x≥f（x）}\end{array}\right.$，求g（x）的值域；
    （3）是否存在实数m，n使得不等式m≤f（x）≤n的解集为[m，n]？若存在，求出m，n的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．设Sn为数列{an}的前n项和，且Sn=n2，数列{bn}为等比数列．已知a1b1+a2b2+a3b3+…+anbn=（n-1）•3n+1+3．
    （Ⅰ）求数列{an}，{bn}的通项公式；
    （Ⅱ）设（an+1）•log3bn+2•cn=1，求证：数列{cn}的前n项和Tn＜$\frac{3}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．在（x3+$\frac{1}{{x}^{2}}$）n的展开式中，若其展开式存在常数项，求n的最小正整数值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=$\left\{\begin{array}{l}{x+1，0≤x＜1}\\{{2}^{x-1}-1，1≤x＜3}\end{array}\right.$，若存在m，n，当0≤m＜n＜3时，有f（m）=f（n），则nf（m）的取值范围是（　　）
    A．[1，3）B．[1，2log23+2）C．[2，3）D．[2，2log23+2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知数列{an}满足a1=2，an+1-an=2（n∈N*），数列{bn}满足b1=4，b3=14，且数列{bn-an}是各项均为正数的等比数列．
    （Ⅰ）求数列{an}和{bn}的通项公式；
    （Ⅱ）令cn=bn-2n，求数列{$\frac{1}{{c}_{n}}$}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知复数z=2i（1-i）（i为虚数单位），z的共轭复数为$\overline{z}$，则$z+\overline{z}$=（　　）
    A．4iB．-4iC．4D．-4

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．若x，y满足约束条件$\left\{\begin{array}{l}x+y≥0\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$，则目标函数z=x-2y的最小值是（　　）
    A．-5B．$-\frac{3}{2}$C．0D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知f（α）=$\frac{tan（π-α）sin（-2π-α）cos（6π-α）}{sin（α+\frac{3}{2}π）cos（α-\frac{1}{2}π）}$
    （1）化简f（α）；
    （2）若sinα=-$\frac{2}{3}$，α∈[一π，-$\frac{π}{2}$]，求f（α）的值．

    查看答案和解析>>

    同步练习册答案