
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0]∪[2,+∞) | B. | (-∞,-2]∪[0,+∞) | C. | [-2,+∞) | D. | [-2,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的最高气温,下面的折线代表可能出现的最低气温.
中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的最高气温,下面的折线代表可能出现的最低气温.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
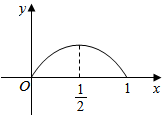 点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )| A. | 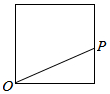 | B. | 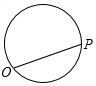 | C. | 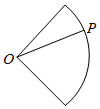 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∨q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com