
���� ���������ײ�Ʒx�֣��Ҳ�Ʒy�֣��г�Լ���������ٸ���Լ������������������z=0.6x+0.8y��������z�ļ�����������ֵ��ֻ�����ֱ��z=0.6x+0.8y���������ڵĵ�ʱ���Ӷ��õ�zֵ���ɣ�
��� �⣺�������ײ�Ʒx�֣��Ҳ�Ʒy�֣�
��x��y����Լ������$\left\{\begin{array}{l}3x+2y��30\\ 0.5x+y��11\\ x��0\\ y��0\end{array}\right.$����4�֣�
��������Ϊz=0.6x+0.8y����Ԫ���� ����5�֣�
������������ͼ��Ӱ���֣������߽磩��
��Ȼz=0.6x+0.8y�ڵ�A��ȡ�����ֵ��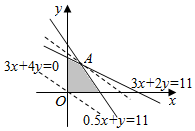 ����9�֣�
����9�֣�
�ɷ�����$\left\{\begin{array}{l}3x+2y=30\\ 0.5x+y=11\end{array}\right.$�����$\left\{\begin{array}{l}x=4\\ y=9\end{array}\right.$����11�֣�
��zmax=0.6��4+0.8��9=9.6�� ����12�֣�
��Ӧ�����ײ�Ʒ4000ǧ�ˣ��Ҳ�Ʒ9000ǧ�˲���ʹ�����������13�֣�
���� �ڽ�����Թ滮��Ӧ����ʱ���䲽��Ϊ���ٷ�����Ŀ��������Ĺ�ϵ���г�����ʽ�飬��Լ������⇒����Լ����������������⇒�۷���Ŀ�꺯��Z��ֱ�߽ؾ�֮��Ĺ�ϵ⇒��ʹ��ƽ��ֱ�߷�������Ž�⇒�ݻ�ԭ����ʵ�����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24�� | B�� | 28�� | C�� | 32�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��0��x��lnx | B�� | ?x��0��x��lnx | C�� | ?x0��0��x0��lnx0 | D�� | ?x0��0��x0��lnx0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{2}$=1 | B�� | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{8}$=1 | C�� | x2-$\frac{{y}^{2}}{4}$=1 | D�� | $\frac{{x}^{2}}{4}$-y2=1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com