
分析 (I)利用等差数列与等比数列的通项公式即可得出.
(II)利用等比数列的通项公式前n项和公式即可得出.
解答 解:(I)数列{an}满足a1=2,an+1-an=2(n∈N*),∴an=2+2(n-1)=2n.
数列{bn}满足b1=4,b3=14,且数列{bn-an}是各项均为正数的等比数列,设其公比为q>0.
b3-a3=(b1-a1)q2,即14-6=(4-2)q2,解得q=2.
∴bn-an=2×2n-1,可得bn=2n+2n.
(II)cn=bn-2n=2n,
∴$\frac{1}{{c}_{n}}$=$(\frac{1}{2})^{n}$.
∴数列{$\frac{1}{{c}_{n}}$}的前n项和Tn=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{n}}$.
点评 本题考查了等差数列与等比数列的通项公式前n项和公式,考查了推理能力与计算能力,属于中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | 96种 | B. | 124种 | C. | 130种 | D. | 150种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的最高气温,下面的折线代表可能出现的最低气温.
中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图(如图),其中上面的折线代表可能出现的最高气温,下面的折线代表可能出现的最低气温.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
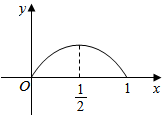 点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )
点P从点O出发,按逆时针方向沿周长为l的图形运动一周,O,P两点连线的距离y与点P走过的路程x的函数关系如图,那么点P所走的图形是( )| A. | 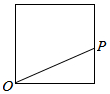 | B. | 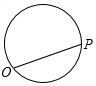 | C. | 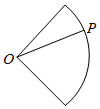 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | $[\frac{1}{3},2]$ | C. | [0,4] | D. | $[\frac{1}{9},4]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4$\sqrt{2}$-5,+∞) | B. | (4$\sqrt{2}$-5,+∞) | C. | (-4$\sqrt{2}$-5,1) | D. | (4$\sqrt{2}$-5,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com