中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图.其中上面的折线代表可能出现的最高气温.下面的折线代表可能出现的最低气温．(Ⅰ)指出最高气温与最低气温的相关性,(Ⅱ)比较最低气温与最高气温方差的大小,(Ⅲ)在[8:00.23:00]内每个整点时刻的温差(最高气温与最低气温的差)依次记为t1.t2.t3.-.t16.求在连续两个时� 题目和参考答案——青夏教育精英家教网—

3．

中国天气网2016年3月4日晚六时通过手机发布的3月5日通州区天气预报的折线图（如图），其中上面的折线代表可能出现的最高气温，下面的折线代表可能出现的最低气温．
（Ⅰ）指出最高气温与最低气温的相关性；
（Ⅱ）比较最低气温与最高气温方差的大小（结论不要求证明）；
（Ⅲ）在[8：00，23：00]内每个整点时刻的温差（最高气温与最低气温的差）依次记为t₁，t₂，t₃，…，t₁₆，求在连续两个时刻的温差中恰好有一个时刻的温差不小于3°的概率．

分析（Ⅰ）由最高气温与最低气温的折线图得到最高气温越高，相应地最低气温也越高．
（Ⅱ）由最高气温曲线波动较小，得到最高气温方差小于最低气温方差．
（Ⅲ）由最高气温与最低气温的折线图列表求出连续两个整点时刻（基本事件）共有15个，其中满足“”恰好有一个时刻的温差不小于3°”的事件（记为A）共有3个，由此能求出在连续两个时刻的温差中恰好有一个时刻的温差不小于3°的概率．

解答解：（Ⅰ）由最高气温与最低气温的折线图得到：
最高气温与最低气温之间成正相关，
即最高气温越高，相应地最低气温也越高．
（Ⅱ）由最高气温与最低气温的折线图得到：
最高气温曲线波动较小，
∴最高气温方差小于最低气温方差．
（Ⅲ）由最高气温与最低气温的折线图可得下表：

整点时刻	8：00	9：00	10：00	11：00	12：00	13：00	14：00	15：00
最高气温	10	11	12	13	13	13	13	12$\frac{2}{3}$
最低气温	4	6	8	10	10$\frac{2}{3}$	11$\frac{1}{3}$	12	0
温差	6	5	4	3	2$\frac{1}{3}$	1$\frac{2}{3}$	1	2$\frac{2}{3}$

整点时刻	16：00	17：00	18：00	19：00	20：00	21：00	22：00	23：00
最高气温	12$\frac{1}{3}$	12	10	8	6	5	4	3
最低气温	8	6	5	4	3	2$\frac{2}{3}$	2$\frac{1}{3}$	2
温差	4$\frac{1}{3}$	6	5	4	3	2$\frac{1}{3}$	1$\frac{2}{3}$	1

由表可知，连续两个整点时刻（基本事件）共有15个：
（8：00，9：00），（9：00，10：00），（10：00，11：00），
（11：00，12：00），（12：00，13：00），（13：00，14：00），
14：00，15：00），（15：00，16：00），（16：00，17：00），
（17：00，18：00），（18：00，19：00），（19：00，20：00），
（20：00，21：00），（21：00，22：00），（22：00，23：00），
其中满足“”恰好有一个时刻的温差不小于3°”的事件（记为A）共有3个，
（11：00，12：00），（15：00，16：00），（20：00，21：00），
∴在连续两个时刻的温差中恰好有一个时刻的温差不小于3°的概率：
P（A）=$\frac{3}{15}=\frac{1}{3}$．

点评本题考查折线图的应用，考查概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：选择题

13．执行如图所示的程序框图，若输出的S的值为$\frac{5}{2}$，则实数k的取值范围为（　　）

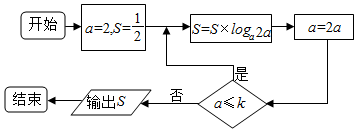
A．

[16，64]

B．

[16，32）

C．

[32，64）

D．

（32，64）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．已知集合A={x|x²+2x-8≥0}，B={x|x²-x-6≤0}，C={x|x²-4ax+3a²≤0}，若A∩B⊆C，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

11．设命题p：?x＞0，x＞lnx．则￢p为（　　）

A．

?x＞0，x≤lnx

B．

?x＞0，x＜lnx

C．

?x₀＞0，x₀＞lnx₀

D．

?x₀＞0，x₀≤lnx₀

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

18．在（x³+$\frac{1}{{x}^{2}}$）ⁿ的展开式中，若其展开式存在常数项，求n的最小正整数值．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

8．已知△ABC中，AC=2，AB=4，AC⊥BC，点P满足$\overrightarrow{AP}$=x$\overrightarrow{AC}$+y$\overrightarrow{AB}$，x+2y=1，则$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）的最小值等于（　　）

A．

-2

B．

-$\frac{28}{9}$

C．

-$\frac{25}{8}$

D．

-$\frac{7}{2}$

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

15．已知数列{a_n}满足a₁=2，a_n+1-a_n=2（n∈N^*），数列{b_n}满足b₁=4，b₃=14，且数列{b_n-a_n}是各项均为正数的等比数列．
（Ⅰ）求数列{a_n}和{b_n}的通项公式；
（Ⅱ）令c_n=b_n-2n，求数列{$\frac{1}{{c}_{n}}$}的前n项和T_n．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

12．已知向量$\overrightarrow{a}$=（x，y），$\overrightarrow{b}$=（-1，2），且$\overrightarrow{a}$+$\overrightarrow{b}$=（1，3），则|$\overrightarrow{a}$-2$\overrightarrow{b}$|等于（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

13．命题“?x＞0，lnx-x≥0”的否定是?x＞0，lnx-x＜0．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学