
【题目】四棱锥S-ABCD的底面为正方形,SD![]() 底面ABCD如下列结论中不正确的是 。
底面ABCD如下列结论中不正确的是 。
A. AB![]() SA
SA
B. BC//平面SAD
C. BC与SA所成的角等于AD与 SC所成的角
D. SA与平面SBD所成的角等于SC与平面SBD所成的角
科目:高中数学 来源: 题型:
【题目】企业需为员工缴纳社会保险,缴费标准是根据职工本人上一年度月平均工资(单位:元)的![]() 缴纳,
缴纳,
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
t | 1 | 2 | 3 | 4 | 5 |
y | 270 | 330 | 390 | 460 | 550 |
某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y(单位:元)与年份序号t的统计如下表:
(1)求出t关于t的线性回归方程![]() ;
;
(2)试预测2019年该员工的月平均工资为多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
(注: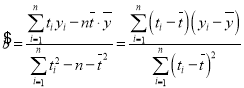 ,
,![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点P的极坐标为![]() ,直线l的极坐标方程为ρcos
,直线l的极坐标方程为ρcos![]() =a,且点P在直线l上.
=a,且点P在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)曲线![]() 的极坐标方程为
的极坐标方程为![]() .若
.若![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,定点
,定点![]() ,
,![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,当点
,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过定点![]() 的直线交曲线
的直线交曲线![]() 于不同的两点
于不同的两点![]() ,
,![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间),且满足
之间),且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知空间几何体ABCDE中,△BCD与△CDE均是边长为2的等边三角形,△ABC是腰长为3的等腰三角形,平面CDE⊥平面BCD,平面ABC⊥平面BCD.
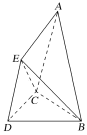
(1)试在平面BCD内作一条直线,使得直线上任意一点F与E的连线EF均与平面ABC平行,并给出证明;
(2)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. “![]() ,若
,若![]() ,则
,则![]() 且
且![]() ”是真命题
”是真命题
B. 在同一坐标系中,函数![]() 与
与![]() 的图象关于
的图象关于![]() 轴对称.
轴对称.
C. 命题“![]() ,使得
,使得![]() ”的否定是“
”的否定是“![]() ,都有
,都有![]() ”
”
D. ![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com