
分析 (1)求出函数的导数,求出导函数的导数,求出导函数的单调区间,从而证明函数的单调性即可;
(2)求出函数的解析式,问题转化为e2x>x2+x+1,由x2+x+1>0,得2x>ln(x2+x+1),设h(x)=2x-ln(x2+x+1),根据函数的单调性求出不等式的解集即可;
(3)令G(x)=e2x-2x2-3x,求出函数的导数,设H(x)=e2x-2x-$\frac{3}{2}$,根据函数的单调性求出G(x)的最小值,从而求出a的最大值即可.
解答 解:(1)证明:f'(x)=2e2x-2x=2(e2x-x),
设g(x)=e2x-x,g'(x)=2e2x-1=0,${e^{2x}}=\frac{1}{2}$,$x=\frac{1}{2}ln\frac{1}{2}$,
x,g′(x),g(x)的变化如下:
| x | (-∞,$\frac{1}{2}$ln$\frac{1}{2}$) | $\frac{1}{2}$ln$\frac{1}{2}$ | ($\frac{1}{2}$ln$\frac{1}{2}$,+∞) |
| g′(x) | - | 0 | + |
| g(x) | ↓ | 极小值 | ↑ |
| x | (0,x0) | x0 | (x0,+∞) |
| G′(x) | - | 0 | + |
| G(x) | ↓ | 极小值 | ↑ |
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道综合题.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
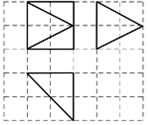 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
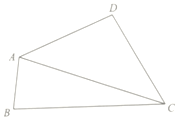 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cos∠D=-$\frac{1}{7}$,AD=DC=2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com