
已知函数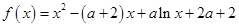 (其中
(其中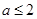 ).
).
(1)求函数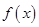 的单调区间;
的单调区间;
(2)若函数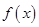 在
在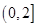 上有且只有一个零点,求实数
上有且只有一个零点,求实数 的取值范围.
的取值范围.
(1)详见解析;(2)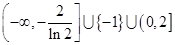 .
.
解析试题分析:(1)先求函数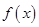 的定义域与导数
的定义域与导数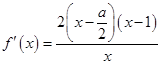 ,对
,对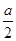 是否在定义域内以及在定义域内与
是否在定义域内以及在定义域内与 进行大小比较,从而确定函数的单调区间;(2)在(1)的条件下结合函数的单调性与零点存在定理对端点值或极值的正负进行限制,从而求出参数
进行大小比较,从而确定函数的单调区间;(2)在(1)的条件下结合函数的单调性与零点存在定理对端点值或极值的正负进行限制,从而求出参数 的取值范围.
的取值范围.
试题解析:(1)函数定义域为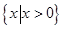 ,
,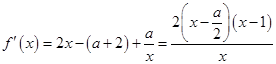 ,
,
①当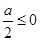 ,即
,即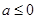 时,
时,
令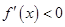 ,得
,得 ,函数
,函数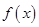 的单调递减区间为
的单调递减区间为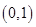 ,
,
令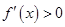 ,得
,得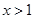 ,函数
,函数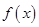 的单调递增区间为
的单调递增区间为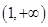 ;
;
②当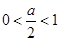 ,即
,即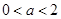 时,
时,
令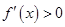 ,得
,得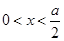 或
或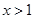 ,函数
,函数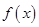 的单调递增区间为
的单调递增区间为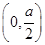 ,
,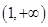 ,
,
令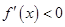 ,得
,得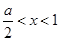 ,函数
,函数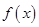 的单调递减区间为
的单调递减区间为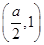 ;
;
③当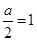 ,即
,即 时,
时, 恒成立,函数
恒成立,函数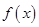 的单调递增区间为
的单调递增区间为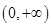 ;
;
(2)①当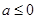 时,由(1)可知,函数
时,由(1)可知,函数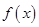 的单调递减区间为
的单调递减区间为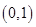 ,
,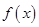 在
在 单调递增,
单调递增,
所以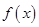 在
在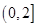 上的最小值为
上的最小值为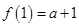 ,
,
由于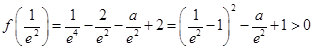 ,
,
要使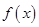 在
在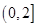 上有且只有一个零点,
上有且只有一个零点,
需满足 或
或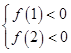 ,解得
,解得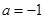 或
或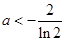 ,
,
所以当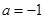 或
或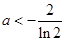 时,
时,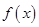 在
在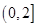 上有且只有一个零点;
上有且只有一个零点;
②当 时,由(1)可知,函数
时,由(1)可知,函数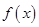 在
在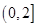 上单调递增,
上单调递增,
且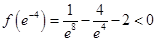 ,
,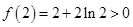 ,
,
所以当 时,
时,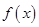 在
在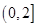 上有且只有一个零点;
上有且只有一个零点;
③当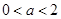 时,由(1)可知,函数
时,由(1)可知,函数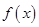 在
在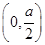 内单调递增,在
内单调递增,在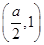 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
又因为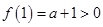 ,所以当
,所以当 时,总有
时,总有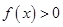 ,
,
因为

科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)当 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)当 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值;
(3)记函数 图象为曲线
图象为曲线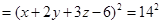 ,设点
,设点 ,
,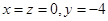 是曲线
是曲线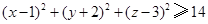 上不同的两点,点
上不同的两点,点 为线段
为线段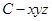 的中点,过点
的中点,过点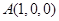 作
作 轴的垂线交曲线
轴的垂线交曲线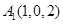 于点
于点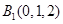 .试问:曲线
.试问:曲线 在点
在点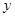 处的切线是否平行于直线
处的切线是否平行于直线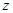 ?并说明理由.
?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, (
( )
)
(1)对于函数 中的任意实数x,在
中的任意实数x,在 上总存在实数
上总存在实数 ,使得
,使得 成立,求实数
成立,求实数 的取值范围
的取值范围
(2)设函数 ,当
,当 在区间
在区间 内变化时,
内变化时,
(1)求函数
 的取值范围;
的取值范围;
(2)若函数
 有零点,求实数m的最大值.
有零点,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
 ,
, 恒成立,求
恒成立,求 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=x2-mlnx,g(x)=x2-x+a.
(1)当a=0时,f(x)≥g(x)在(1,+∞),上恒成立,求实数m的取值范围;
(2)当m=2时,若函数h(x)=f(x)-g(x)在[1,3]上恰有两个不同的零点,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com