
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 由向量数量积的性质,向量的平方即为模的平方,可得|$\overrightarrow{a}$+$\overrightarrow{b}$|,再由向量数量积的定义和余弦函数的有界性,即可得到所求最大值.
解答 解:向量$|{\overrightarrow a}|=\sqrt{2},|{\overrightarrow b}|=1,|{\overrightarrow c}|=\sqrt{3}$,且$\overrightarrow a•\overrightarrow b=0$,
可得|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$=$\sqrt{2+0+1}$=$\sqrt{3}$.
则$\overrightarrow{a}$?$\overrightarrow{c}$+$\overrightarrow{b}$?$\overrightarrow{c}$=($\overrightarrow{a}$+$\overrightarrow{b}$)?$\overrightarrow{c}$=$\sqrt{3}$?$\sqrt{3}$cos<$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{c}$>≤3.
当且仅当$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{c}$同向共线,可得最大值3.
故选:D.
点评 本题考查向量的数量积的定义和性质,主要是向量的平方即为模的平方,考查余弦函数的有界性,属于中档题.


科目:高中数学 来源: 题型:解答题
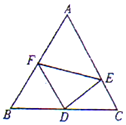 如图,在边长为2的正三角形△ABC中,D为BC的中点,E,F分别在边CA,AB上.
如图,在边长为2的正三角形△ABC中,D为BC的中点,E,F分别在边CA,AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.
如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 当前襄阳市正在积极创建文明城市,市某交警支队为调查市民文明驾车的情况,在市区某路口随机检测了40辆车的车速.现将所得数据分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),并绘得如图所示的频率分布直方图.
当前襄阳市正在积极创建文明城市,市某交警支队为调查市民文明驾车的情况,在市区某路口随机检测了40辆车的车速.现将所得数据分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),并绘得如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月份i | 1 | 2 | 3 | 4 | 5 | 6 |
| 单价xi(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi(件) | 11 | 10 | 8 | 6 | 5 | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com