
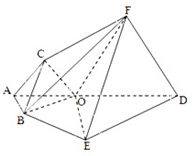
 如图,ABCDEF为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
如图,ABCDEF为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.分析 (Ⅰ)设G是线段DA与EB延长线的交点.由已知条件推导出OB,OC,的关系,然后证明BC∥EF.
(Ⅱ)求出棱锥的底面面积,求出四棱锥F-OBED的高,然后求解几何体的体积.
解答 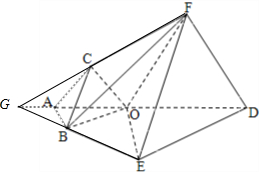 (Ⅰ)证明:设G是线段DA与EB延长线的交点.
(Ⅰ)证明:设G是线段DA与EB延长线的交点.
由于△OAB与△ODE都是正三角形,
∴OB$\stackrel{∥}{=}$$\frac{1}{2}$DE,OG=OD=2,
同理,设G'是线段DA与FC延长线的交点,有OG'=OD=2.
又由于G和G'都在线段DA的延长线上,
∴G与G'重合.在△GED和△GFD中,
由OB$\stackrel{∥}{=}$$\frac{1}{2}$DE和OC$\stackrel{∥}{=}$$\frac{1}{2}$DF,
知B和C分别是GE和GF的中点.
∴BC是△GEF的中位线,
故BC∥EF.
(Ⅱ)由OB=1,OE=2.∠EOB=60°,可知:${S}_{△EOB}=\frac{\sqrt{3}}{2}$,而△OED是边长为2的正三角形,
所以,${S}_{△OED}=\sqrt{3}$所以${S}_{△BED}=\frac{3\sqrt{3}}{2}$,过点F作FQ⊥AD,交AD于Q,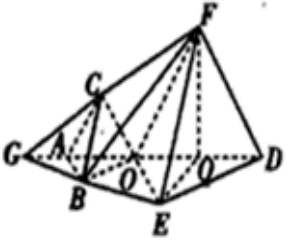
由平面ABED⊥平面ACFD可知FQ是四棱锥F-OBED的高,且FQ=$\sqrt{3}$.
所以${V}_{F-OBED}=\frac{1}{3}FQ•{S}_{OBED}$=$\frac{3}{2}$.
点评 本题考查直线与平面平行的性质定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,$\frac{3}{2}$) | B. | [-$\frac{1}{2}$,$\frac{3}{2}$] | C. | (-$\frac{3}{2}$,$\frac{1}{2}$) | D. | [-$\frac{3}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{17}$ | B. | $\frac{9}{19}$ | C. | $\frac{10}{21}$ | D. | $\frac{11}{23}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z | B. | x=km,k∈Z | C. | x=km+$\frac{π}{2}$,k∈Z | D. | x=$\frac{kπ}{2}$,k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 9 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com