
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
分析 (1)根据所给的这组数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式,求得结果,再把样本中心点代入,求出a的值,得到线性回归方程.
(2)根据所给的这组数据,代入相关指数公式,可求出R2,
(3)根据计算的R2的大小进行分析
(4)根据上一问所求的线性回归方程,把x=100代入线性回归方程,即可估计生产100吨甲产品的生产能耗
解答 解:(1)对照数据,计算得 $\sum _{i=1}^{4}{{x}_{i}}^{2}$=86,$\sum _{i=1}^{4}{{x}_{i}{y}_{i}}^{\;}$=66.5,$\overline{x}$=4.5,$\overline{y}$=3.5,
∴回归方程的系数为$\hat{b}$=$\frac{66.5-4×4.5×3.5}{86-4×{4.5}^{2}}$=0.7,$\hat{a}$=0.35,
∴所求线性回归方程为$\hat{y}$=0.7x+0.35,
R2=1-$\frac{\sum _{i=1}^{4}{({y}_{i}-\widehat{{y}_{i}})}^{2}}{\sum _{i=1}^{4}{({y}_{i}-\overline{y})}^{2}}$=1-$\frac{0.0025+0.0225+0.0225+0.0025}{1+0.25+0.25+1}$=1-0.02=0.98.
(3)∵R2=0.98,非常接近1,故用回归方程$\hat{y}$=0.7x+0.35模拟x,y间的关系的拟合效果非常好
(4)由(1)求出的线性回归方程,估计生产100吨甲产品的生产能耗为0.7×100+0.35=70.35(吨),
∴估计生产100吨甲产品的生产能耗为70.35吨.
点评 本题考查线性回归方程,两个变量之间的关系,除了函数关系,还存在相关关系,通过建立回归直线方程,就可以根据其部分观测值,获得对这两个变量之间整体关系的了解.


科目:高中数学 来源: 题型:选择题
| A. | [${\frac{1}{2}$,2) | B. | [1,4] | C. | [${\frac{1}{4}$,4) | D. | [${\frac{1}{2}$,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
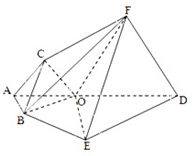 如图,ABCDEF为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
如图,ABCDEF为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
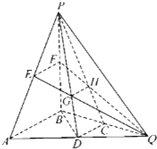 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连接GH.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=b b=a | B. | c=b b=a a=c | C. | b=a a=b | D. | a=c c=b b=a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | ($\frac{1}{2}$,2] | C. | [-1,$\frac{1}{2}$) | D. | (-∞,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com