
分析 由已知求得$\overrightarrow{a}•\overrightarrow{b}$,再由向量垂直与数量积的关系列式求得λ值.
解答 解:由|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{2}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为45°,得
$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos45°=2×\sqrt{2}×\frac{\sqrt{2}}{2}=2$.
∵λ$\overrightarrow{b}$-$\overrightarrow{a}$与$\overrightarrow{a}$垂直,
∴(λ$\overrightarrow{b}$-$\overrightarrow{a}$)•$\overrightarrow{a}$=$λ\overrightarrow{a}•\overrightarrow{b}-|\overrightarrow{a}{|}^{2}=2λ-4=0$,
∴λ=2.
故答案为:2.
点评 本题考查平面向量的数量积运算,熟记数量积公式是关键,是基础题.


科目:高中数学 来源: 题型:解答题
 如图,四棱锥S-ABCD,SA⊥平面ABCD,E是SC的中点,AD=AB=2,CD=CB=2$\sqrt{3}$,AC=4,SA=2$\sqrt{2}$.
如图,四棱锥S-ABCD,SA⊥平面ABCD,E是SC的中点,AD=AB=2,CD=CB=2$\sqrt{3}$,AC=4,SA=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{2}{9}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
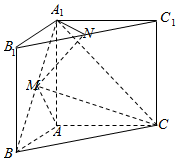 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a、b、c均不为0 | B. | a、b、c中至少有一个为0 | ||
| C. | a、b、c中至多有一个为0 | D. | a、b、c中至少有一个不为0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com