
分析 (1)令f(x)=(1+$\frac{a}{x}$)ex=0得1+$\frac{a}{x}$=0,从而讨论方程是否有解即可;
(2)求导f′(x)=(1+$\frac{a}{x}$-$\frac{a}{{x}^{2}}$)ex=ex$\frac{{x}^{2}+ax-a}{{x}^{2}}$,从而判断导数的正负,从而确定函数的单调区间;
(3)结合(2)知f(x)的单调增区间为(-∞,$\frac{-a-\sqrt{{a}^{2}+4a}}{2}$),单调减区间为($\frac{-a-\sqrt{{a}^{2}+4a}}{2}$,-$\frac{a}{2}$];且$\underset{lim}{x→-∞}$(1+$\frac{a}{x}$)ex=0,f(-$\frac{a}{2}$)=-${e}^{-\frac{a}{2}}$<0,从而确定答案.
解答 解:(1)令f(x)=(1+$\frac{a}{x}$)ex=0得,
1+$\frac{a}{x}$=0,
①当a≤0时,1+$\frac{a}{x}$≥1,故方程1+$\frac{a}{x}$=0无解,
②当a>0时,x=-a;
故当a≤0时,函数f(x)在其定义域上没有零点,
当a>0时,函数f(x)在其定义域上的零点为-a.
(2)∵f(x)=(1+$\frac{a}{x}$)ex,
∴f′(x)=(1+$\frac{a}{x}$-$\frac{a}{{x}^{2}}$)ex=ex$\frac{{x}^{2}+ax-a}{{x}^{2}}$,
①当a≤0时,1+$\frac{a}{x}$-$\frac{a}{{x}^{2}}$>0在(-∞,0)上恒成立,
∴函数f(x)的单调增区间为(-∞,0);
②当a>0时,解方程x2+ax-a=0得,
x1=$\frac{-a-\sqrt{{a}^{2}+4a}}{2}$,x2=$\frac{-a+\sqrt{{a}^{2}+4a}}{2}$>0(舍去);
故当x∈(-∞,$\frac{-a-\sqrt{{a}^{2}+4a}}{2}$)时,f′(x)>0,
当x∈($\frac{-a-\sqrt{{a}^{2}+4a}}{2}$,0)时,f′(x)<0,
故f(x)的单调增区间为(-∞,$\frac{-a-\sqrt{{a}^{2}+4a}}{2}$),单调减区间为($\frac{-a-\sqrt{{a}^{2}+4a}}{2}$,0);
(3)当a>0时,-$\frac{a}{2}$>$\frac{-a-\sqrt{{a}^{2}+4a}}{2}$,
故f(x)的单调增区间为(-∞,$\frac{-a-\sqrt{{a}^{2}+4a}}{2}$),单调减区间为($\frac{-a-\sqrt{{a}^{2}+4a}}{2}$,-$\frac{a}{2}$];
且$\underset{lim}{x→-∞}$(1+$\frac{a}{x}$)ex=0,f(-$\frac{a}{2}$)=-${e}^{-\frac{a}{2}}$<0,
故函数f(x)在区间(-∞,-$\frac{a}{2}$]上是存在最小值为-${e}^{-\frac{a}{2}}$.
点评 本题考查了导数的综合应用及函数的最值的求法.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-3,-2) | B. | (-1,0) | C. | (0,1) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
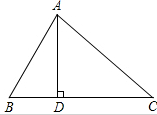 如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.
如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 4 | C. | -4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com