
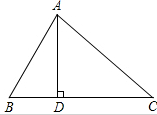
 如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.
如图,在△ABC中,AD⊥BC,$\frac{\overrightarrow{AB}}{|\overrightarrow{AB|}}$•$\frac{\overrightarrow{AC}}{|\overrightarrow{AC|}}$=$\frac{\sqrt{2}}{2}$,BD=4,CD=6.分析 (1)根据向量夹角的余弦公式即可得到cos$∠BAC=\frac{\sqrt{2}}{2}$,从而便得出$∠BAC=\frac{π}{4}$;
(2)可设AD=x,从而可表示出$AB=\sqrt{{x}^{2}+16},AC=\sqrt{{x}^{2}+36}$,而又知道cos$∠BAC=\frac{\sqrt{2}}{2}$,BC=10,从而可根据余弦定理建立关于x的方程,解方程便可得出x值,从而便可得出AC,AB的长.
解答 解:(1)$cos∠BAC=\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}=\frac{\sqrt{2}}{2}$;
∴$∠BAC=\frac{π}{4}$;
(2)设AD=x,则$AB=\sqrt{16+{x}^{2}},AC=\sqrt{36+{x}^{2}}$,cos$∠BAC=\frac{\sqrt{2}}{2}$,BC=10;
∴在△ABC中,由余弦定理得:AB2+AC2-2AB•AC•cos∠BAC=BC2;
即$16+{x}^{2}+36+{x}^{2}-\sqrt{2}•\sqrt{16+{x}^{2}}•\sqrt{36+{x}^{2}}=100$;
整理得:$2({x}^{2}-24)=\sqrt{2}•\sqrt{16+{x}^{2}}•\sqrt{36+{x}^{2}}$,两边平方并整理得:
x4-148x2+4•144=0;
解得x2=144,或x2=4;
∵x2>24;
∴x2=144;
∴$AB=\sqrt{16+144}=40$,;
∴$AB=\sqrt{16+144}=4\sqrt{10},AC=\sqrt{36+144}=6\sqrt{5}$;
即边AC,AB的长分别为$6\sqrt{5},4\sqrt{10}$.
点评 考查向量夹角的余弦公式,已知三角函数值求角,以及直角三角形边的关系,余弦定理,解一元二次方程.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | $\frac{129}{4}$ | C. | 64 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com