
【题目】函数f(x)= ![]() +log2(6﹣x)的定义域是( )
+log2(6﹣x)的定义域是( )
A.{x|x>6}
B.{x|﹣3<x<6}
C.{x|x>﹣3}
D.{x|﹣3≤x<6}
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD= ![]() .
. 
(1)求证:平面PQB⊥平面PAD;
(2)若PM=3MC,求二面角M﹣BQ﹣C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李从网上购买了一件商品,快递员计划在下午5:00-6:00之间送货上门,已知小李下班到家的时间为下午5:30-6:00.快递员到小李家时,如果小李未到家,则快递员会电话联系小李.若小李能在10分钟之内到家,则快递员等小李回来;否则,就将商品存放在快递柜中.则小李需要去快递柜收取商品的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.
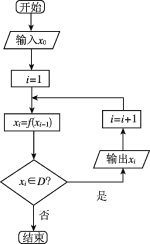
(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,点![]() 坐标是
坐标是![]() ,曲线
,曲线![]() 的方程为
的方程为![]() ;以极点为坐标原点,极轴为
;以极点为坐标原点,极轴为![]() 轴的正半轴建立平面直角坐标系,斜率是
轴的正半轴建立平面直角坐标系,斜率是![]() 的直线
的直线![]() 经过点
经过点![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求证直线![]() 和曲线
和曲线![]() 相交于两点
相交于两点![]() 、
、![]() ,并求
,并求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(9),f(27)的值
(2)解不等式f(x)+f(x﹣8)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种商品的经验表明,该商品每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (单位:元/千克)满足关系式
(单位:元/千克)满足关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为7元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为7元/千克时,每日可售出该商品11千克.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若该商品的成本为5元/千克,试确定销售价格![]() 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com