
【题目】已知函数f(x)=![]() (a∈R)是奇函数.
(a∈R)是奇函数.
(1)求实数a的值;
(2)判断并证明f(x)在R上的单调性.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求证:方程![]() 有实根;
有实根;
(2)![]() 在
在![]() 上是单调递减函数,求实数
上是单调递减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 的解集为空集,求所有满足条件的实数
的解集为空集,求所有满足条件的实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数f(x)=Asin(ωx+![]() )(ω>0,|
)(ω>0,|![]() |<
|<![]() )在某一个周期内的图象时,列表并填入了部分数据,如表:
)在某一个周期内的图象时,列表并填入了部分数据,如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 2 | -2 | 0 |
(1)请将上表数据补充完整,填写在答题卷上相应位置,并直接写出函数f(x)的解析式;
(2)若f(![]() )=
)=![]() ,求cos(2α+
,求cos(2α+![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为![]() 80,90
80,90![]() 、
、![]() 90,100
90,100![]() 、
、![]() 100,110
100,110![]() 、
、![]() 110,120
110,120![]() 、
、![]() 120,130
120,130![]() ,由此得到两个班测试成绩的频率分布直方图:
,由此得到两个班测试成绩的频率分布直方图:
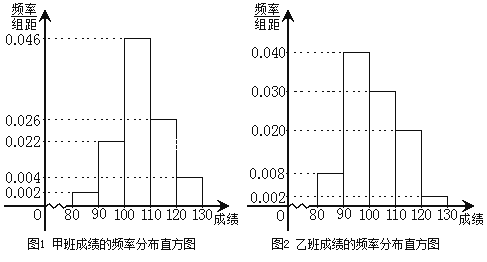
(1)完成下面2×2列联表,你能有97.5![]() 的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 |
|
| 50 |
乙班 |
|
| 50 |
合计 |
|
| 100 |
(2)根据所给数据可估计在这次测试中,甲班的平均分是105.8,请你估计乙班的平均分,并计算两班平均分相差几分?
附:
![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣a|, (Ⅰ)若a=4,求f(x)≤x的解集;
(Ⅱ)若f(x+1)>|2﹣a|对x∈(0,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)为了解某校今年高一年级女生的身体素质状况,从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试,成绩低于5米为不合格,成绩在5至7米(含5米不含7米)的为及格,成绩在7米至11米(含7米和11米,假定该校高一女生掷铅球均不超过11米)为优秀.把获得的所有数据,分成![]() 五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.
五组,画出的频率分布直方图如图所示.已知有4名学生的成绩在9米到11米之间.

(1)求实数![]() 的值及参加“掷铅球”项目测试的人数;
的值及参加“掷铅球”项目测试的人数;
(2)若从此次测试成绩最好和最差的两组中随机抽取2名学生再进行其它项目的测试,求所抽取的2名学生自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+alnx(a∈R).
(1)讨论函数f(x)的单调性;
(2)若函数f(x)有两个极值点x1 , x2(x1<x2),且不等式f(x1)≥mx2恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com