
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
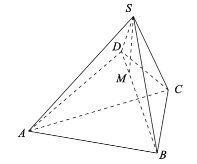
(1)求证:![]() ;
;
(2)若![]() 为线段
为线段![]() 上的一点,
上的一点,![]() ,
,![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)设![]() 交
交![]() 于点
于点![]() ,证明
,证明![]() 平面
平面![]() 内的两条相交直线即可得到线面垂直,再由线面垂直的性质,可证明线线垂直;
内的两条相交直线即可得到线面垂直,再由线面垂直的性质,可证明线线垂直;
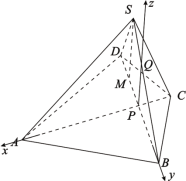
(2)找到三条两两互相垂直的直线,以![]() 为原点,以射线
为原点,以射线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正半轴建立空间直角坐标系,求出平面
轴正半轴建立空间直角坐标系,求出平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,求法向量夹角的余弦值,即可求得答案.
,求法向量夹角的余弦值,即可求得答案.
设![]() 交
交![]() 于点
于点![]() ,
,![]()
![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,在
,在![]() 中,
中,
![]() 且
且![]() ,得
,得![]() ,即
,即![]() ,
,
又平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]()
![]()
(2)平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
以![]() 为原点,以射线
为原点,以射线![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴正半轴建立空间直角坐标系,
轴正半轴建立空间直角坐标系,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则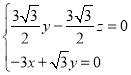 ,
,
取![]() ,得
,得![]()
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,取
,取![]() ,得
,得![]() ,
,
设所求角为![]() ,则
,则![]() ,
,
![]() 所求的锐二面角余弦值为
所求的锐二面角余弦值为![]()


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
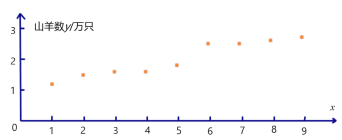
【题目】某县畜牧技术员张三和李四![]() 年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量
年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() (单位:万只)与相应年份
(单位:万只)与相应年份![]() (序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
(序号)的数据表和散点图(如图所示),根据散点图,发现y与x有较强的线性相关关系.
年份序号 |
|
|
|
|
|
|
|
|
|
年养殖山羊 |
|
|
|
|
|
|
|
|
|
(1)根据表中的数据和所给统计量,求![]() 关于
关于![]() 的线性回归方程(参考统计量:
的线性回归方程(参考统计量:![]() ,
,![]() ;
;
(2)李四提供了该县山羊养殖场的个数![]() (单位:个)关于
(单位:个)关于![]() 的回归方程
的回归方程![]() .
.
试估计:①该县第一年养殖山羊多少万只?
②到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:![]()
![]()
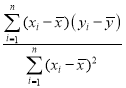 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为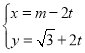 (
(![]() ,
,![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为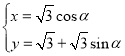 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,求曲线
轴正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程;
的极坐标方程;
(2)若![]() ,点
,点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
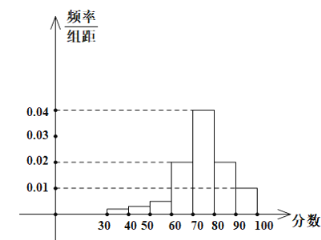
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数),将曲线
为参数),将曲线![]() 上所有点横坐标缩短为原来的
上所有点横坐标缩短为原来的![]() ,纵坐标不变,得到曲线
,纵坐标不变,得到曲线![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求曲线![]() 的参数方程和
的参数方程和![]() 的取值范围;
的取值范围;
(2)求![]() 中点
中点![]() 的轨迹的参数方程.
的轨迹的参数方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装加工厂为了提高市场竞争力,对其中一台生产设备提出了甲、乙两个改进方案:甲方案是引进一台新的生产设备,需一次性投资1000万元,年生产能力为30万件;乙方案是将原来的设备进行升级改造,需一次性投入700万元,年生产能力为20万件.根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,无论是引进新生产设备还是改造原有的生产设备,设备的使用年限均为6年,该产品的销售利润为15元/件(不含一次性设备改进投资费用).
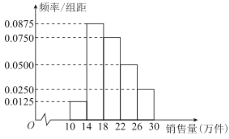
(1)根据年销售量的频率分布直方图,估算年销量的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立.
①根据频率分布直方图估计年销售利润不低于270万元的概率:
②若以该生产设备6年的净利润的期望值作为决策的依据,试判断该服装厂应选择哪个方案.(6年的净利润=6年销售利润-设备改进投资费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车因绿色、环保、健康的出行方式,在国内得到迅速推广.最近,某机构在某地区随机采访了10名男士和10名女士,结果男士、女士中分别有7人、6人表示“经常骑共享单车出行”,其他人表示“较少或不选择骑共享单车出行”.
(1)从这些男士和女士中各抽取一人,求至少有一人“经常骑共享单车出行”的概率;
(2)从这些男士中抽取一人,女士中抽取两人,记这三人中“经常骑共享单车出行”的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com