
分析 (1)将直线l极坐标方程转化成直角坐标,设P点坐标,利用点到直线的距离公式及辅助角公式,根据余弦函数的性质,即可求得点P到直线l的距离的最大值;
(2)由题意可知:?t∈R,acost-2sint+4>0恒成立,利用辅助角公式,只需$\sqrt{{a}^{2}+4}$<4,即可求得a的取值范围.
解答 解:(1)由$ρcos({θ+\frac{π}{4}})=-2\sqrt{2}$,得$\frac{\sqrt{2}}{2}$(ρcosθ-ρsinθ)=-2$\sqrt{2}$,
化成直角坐标方程得$\frac{\sqrt{2}}{2}$(x-y)=-2$\sqrt{2}$,
∴直线l的方程为x-y+4=0,依题意,设P(2$\sqrt{3}$cost,2sint),
则P到直线l的距离d=$\frac{丨2\sqrt{3}cost-2sint+4丨}{\sqrt{2}}$=$\frac{丨4cos(t+\frac{π}{6})+4丨}{\sqrt{2}}$=2$\sqrt{2}$+2$\sqrt{2}$cos(t+$\frac{π}{6}$),
当t+$\frac{π}{6}$=2kπ,即t=2kπ-$\frac{π}{6}$,k∈Z时,dmax=4$\sqrt{2}$,
故点P到直线l的距离的最大值为4$\sqrt{2}$.
(2)因为曲线C上的所有点均在直线l的右下方,
?t∈R,acost-2sint+4>0恒成立,即$\sqrt{{a}^{2}+4}$cos (t+φ)+4>0(其中tanφ=$\frac{2}{a}$)恒成立,
∴$\sqrt{{a}^{2}+4}$<4,又a>0,解得0<a<2$\sqrt{3}$,
故a取值范围(0,2$\sqrt{3}$).
点评 本题考查直线的极坐标方程与直角坐标方程的转化,考查点到直线的距离公式,余弦函数的性质,考查不等式恒成立,考查计算能力,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,0),(0,-2) | B. | (0,1),(-1,0) | C. | (0,-1),(1,0) | D. | (0,3),(-3,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知A,B分别是射线CM,CM(不含端点C)上运动,在△ABC中,角A,B,C所对的边分别为a,b,c.
已知A,B分别是射线CM,CM(不含端点C)上运动,在△ABC中,角A,B,C所对的边分别为a,b,c.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
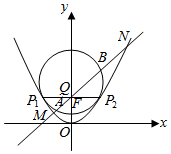 如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.
如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com