Question

17．定义域为R的偶函数f（x）满足对任意x∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x²+12x-18，若函数y=f（x）-log_a（x+1）在（0，+∞）上恰有三个零点，则a的取值范围是（　　）

• A． （0，$\frac{{\sqrt{2}}}{2}$）
• B． （0，$\frac{{\sqrt{3}}}{3}$）
• C． （0，$\frac{{\sqrt{5}}}{5}$）
• D． （$\frac{{\sqrt{5}}}{5}$，$\frac{{\sqrt{3}}}{3}$）

Answer 1

分析 由题意可求得f（1）=0，从而函数y=f（x）-log_a（x+1）在（0，+∞）上恰有三个零点可化为函数y=f（x）与y=log_a（x+1）在（0，+∞）上有三个不同的交点，从而由图象解出a的取值范围．

解答 解：∵f（x+2）=f（x）-f（1），
∴f（1）=f（-1）-f（1），
又∵f（x）是偶函数，
∴f（1）=0，
函数f（x）是以2为周期的偶函数，
函数y=f（x）-log_a（x+1）在（0，+∞）上恰有三个零点可化为
函数y=f（x）与y=log_a（x+1）在（0，+∞）上有三个不同的交点，
作函数y=f（x）与y=log_a（x+1）的图象如下，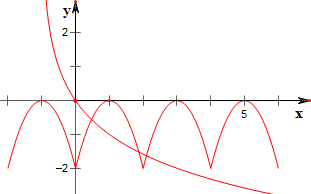

结合函数图象知，
$\left\{\begin{array}{l}{lo{g}_{a}（2+1）＞-2}\\{lo{g}_{a}（4+1）＜-2}\end{array}\right.$，
解得，$\frac{{\sqrt{5}}}{5}$＜a＜$\frac{{\sqrt{3}}}{3}$；
故选D．

点评 本题考查了函数的图象的作法与函数的零点的求法，属于基础题．